新型电流模式积分电路设计

）中λ为面积比系数。

　　当λ=1时，跨导线性原理可表示为：

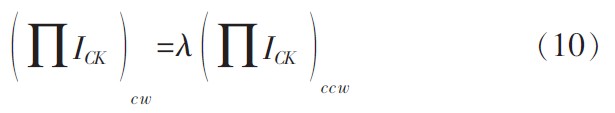
　　式（10）表明，在λ=1的条件下，TL环路中顺时针方向集电级电流之积等于逆时针的集电极电流之积，这是跨导线性原理最简洁的表达形式。

 

 

 

 

　　1.2 CCCII的电路符号和端口特性

　　CCCII的输入输出端口特性可用矩阵式来表示：

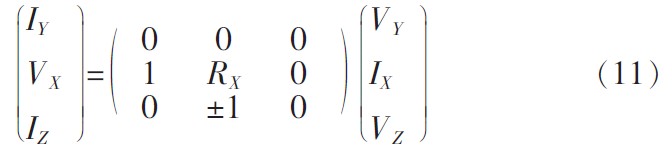
　　X端为电流输入端，Y端为电压输入端，输入电流为零；与CCII相同的是X端电压不是精确跟随Y端输入电压，而是与X端寄生电阻有关。

图2 CCCII电路符号

　　矩阵中的正负号分别代表CCCII+和CCCII-,对CCCII+而言，IX=+IY,对CCCII-而言，IZ=-IX,RX为X端口的寄生电阻，受CCCII内部的偏置电流IB控制。CCCII的电路符号和零极子表示方法如图3所示。

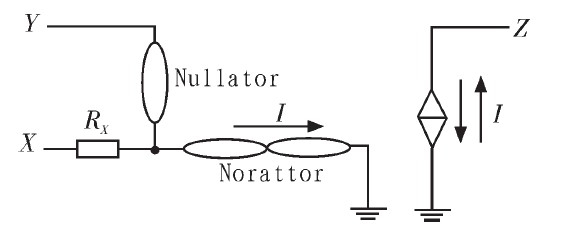
图3 CCCII零极子表示方法

　　2 共源共栅CCCII设计

　　2.1 共源共栅电流镜

　　在电流传输器中，电流镜是必不可少的电路模型。通常的来说，期望一个电流镜能够拥有较高的电流传输精度，较高的输出电阻，较低的输入电压以及最小的输出电压。

　　图4所示的基本电流镜号模型，由于自身沟道长度的调制效应，很难达到较高的电流传输精度及较高的输出电阻。图5中所示的共源共栅电流镜则能获得比普通电流镜更高的电流传输精度和输出电阻。

图4 基本电路镜

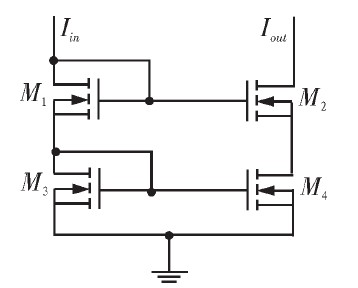
图5 共源共栅电流镜

　　2.2 共源共栅电流镜CMOS CCCII设计电路

　　图6为基于基本电流镜的CCCII电路，它包括了M1~M4组成的跨导电路，以及M5~M6,M7~M8,M10~M11,M12~M13的基本电流镜。基本电流镜M5~M6,M9~M11向跨导电路提供偏置电流IB,由于基本电流镜输出阻抗低，因此偏置电流IB传输到跨导线性电路的比例较少。输出端Z与基本电流镜输出端相连，输出阻抗较低。

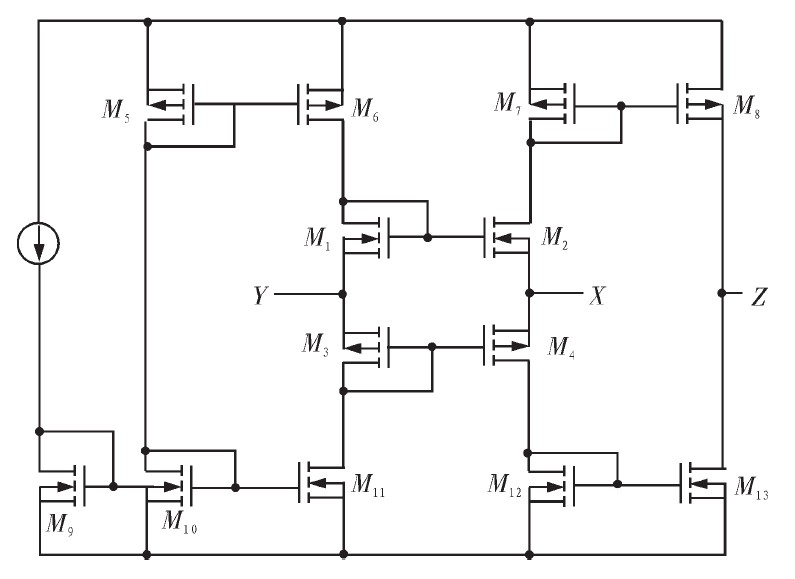
图6 基于基本电流镜的CCCII电路

　　用共源共栅电流镜能实现如图7的CMOS CCCII电流传输器电路，M1~M4构成跨导线性环路实现电压跟随器，M9~M12,M17~M12组成同相传送电路，将X端电流IX镜像耦合到IZ.而M5~M8,M13~M16构成放大倍数为1的电流镜，为跨导线性环路提供直流偏置。将基本电流镜改为共源共栅电流镜，不仅能增大输出阻抗，而且能增大传输精度。

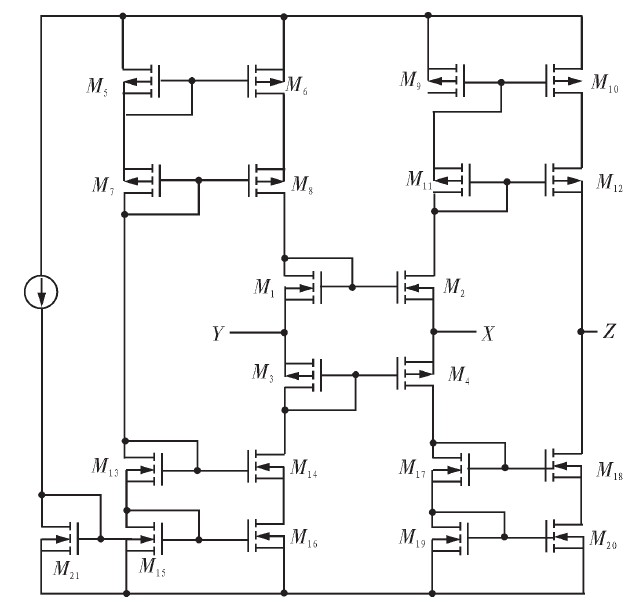
图7 基于共源共栅电流镜的CCCII

　　2.3 共源共栅CMOS CCCII性能仿真

　　基于TMSC0.18umCMOS工艺参数，运用HSPICE软件仿真，对共源共栅COMS CCCII电流传输器进行性能仿真，电路采用1.5 V电压供电。由矩阵关系，首先观察IZ随着IX的变化情况。

　　可以看出，如同理论推导中所体现的一样，在没有任何电流误差的情况下，可以得到较高的传输精度，可以观察导IZ随着IX变化而变化，较好的跟随了IX.

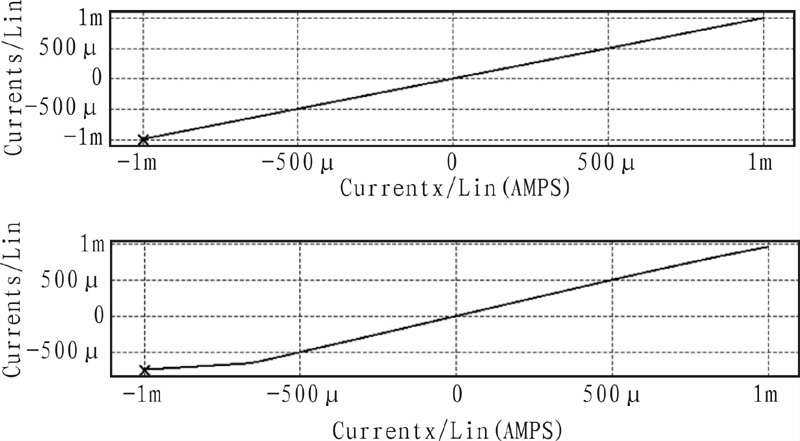
图8 IZ随着IX变化

　　3 电流模式积分电路设计与仿真

　　3.1 电流模积分器设计

　　在共源共栅COMS CCCII的基础上，在X端添加电阻，在Y端添加电容，并改为电流输入端就可以够成一个电流模式的积分电路。示意图如图9所示。

图9 CCCII电流模式积分器

　　假设电容C初始电压为零，则根据CCCII端口特性得到：

　　上式表明，输出电流I0为输入对时间的积分。

　　3.2 电流模积分器仿真

　　基于TMSC0.18μmCMOS工艺参数，运用HSPICE软件仿真，对电流模积分器分别输入典型正弦激励和方波激励进行了电路仿真。

　　当给积分器输入正弦波时，输入输出波形如图10所示。

图10 正弦波积分

　　当给积分器输入方波时，输入输出波形如图11所示。

图11 方波积分

　　最后仿真了积分器的频率响应特性，如图12所示。

图12 积分器频率响应特性

　　通过公示分析，当激励源分别采用正弦信号以及方波信号时，积分电路的输出结果应该为余弦信号以及三角波信号。由图8和图9可得，此积分电路的运算结果同理论结果具有良好的一致性，从而证明了此积分电路设计的正确性。

　　4 结论

　　电流控制电流传输器已经是电流模式电路中非常常用的模块之一，本文提出了基于共源共栅COMS CCCII电流传输器，提高了输出阻抗和电流传输精度，并且基于此CCCII电路设计了电流模式积分电路。在采用TMSC0.18μmCMOS工艺参数，运用HSPICE软件仿真，仿真结果验证了共源共栅电流传输器的传输精度，输出阻抗及可行性，并且在激励源采用正弦，方波信号的情况下，对于此积分电路进行了验证，仿真结果显示具有较高的精度。因此，该积分电路在很多应用中可以替代传统的积分电路，具有广泛的应用前景。