新型电流模式积分电路设计

　　摘要：介绍了电流模式电路的基本概念和发展概况，与电压模式电路相比较，电流模式电路的主要性能特点。并介绍了广泛应用于各种电流模式电路的第二代电流控制电流传输器原件的跨导线性环特性和端口特性，以及其基本组成共源共栅电流镜，并提出了基于共源共栅电流镜的新型COMS电流传输器。在此基础上，设计了基于电流控制电流传输器的电流模式积分电路，并利用Hspice软件进行输入为正弦波和方波时的输出波形的仿真验证。

　　在模拟电子电路中，人们长久以来习惯于采用电压作为信号变量，并通过处理电压信号来决定电路的功能。因此促成了大量电压信号处理电路，或者称为电压模式电路的诞生和发展。

　　但是，随着被处理信号的频率越来越高，电压型运算放大器的固有缺点开始阻碍它在高频、高速环境中的应用。电压型运算放大器的缺点之一，它在-3 dB闭环宽带与闭环增益的乘积是常数，当宽带向高频区域扩展时，增益成比例下降；缺点之二，它在大信号下输出电压的最高转换速率很低，一般只有0.2~20 V/μs.

　　在近些年来，以电流为信号变量的电流在信号处理中的巨大潜在优点被发现被挖掘出来，促成了一种新型电路--电流模式电路的发展。人们发现，电流模式电路可以解决电压模式电路所遇到的一系列难题，在速度、带宽、动态范围等方面获得更加优良的性能。

　　1 第二代电流控制电流传输器 CCCII

　　第二代电流控制电流传输器元件起源CCII,但是由于CCII内部电路的输入端X端与Y端存在一个寄生电阻，而传输特性并没有考虑这个电阻，从而造成CCII的X端与Y端的电压跟踪无法达到理想的程度，而CCCII就是利用X端的寄生电阻受到内部直流偏压控制的特性以达到电压可调的特性。

　　1996年，学者Alain Fabre等人基于跨导线性环特性提出了第二代电流控制电流传输器电路，而随后的CCCII电路基本上也都是基于跨导线性环特性实现的。

　　1.1 线性跨导原理

　　跨导线性电路的主要性能是借助于双极性晶体管的跨导参数与其集电极电流成正比关系得到的。跨导参数与其集电极电流之间的比例关系为：在一个含有偶数个正向偏置发射结，且排列成顺时针方向结的数目和反时针方向结的数目相等的闭环中，顺时针方向发射电流密度之积等于反时针方向发射结电流密度之积。

　　对于双极性晶体管，集电极电流Ic与基-射结电压VBE之间的关系是它的核心关系。这种关系可以表示为：

　　式（1）中：VT是热电压，在常温下其值约26 mV;反向饱和电流，它对温度敏感，每提高1摄氏度增加约9.5%,同时，近似于发射区面积成正比。对式（1）求微分，可以得到：

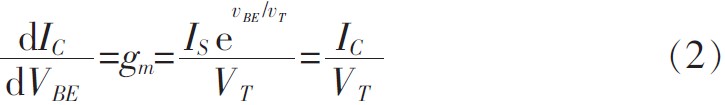
　　式（2）表明，理想BJT的跨导gm是集电极静态电流的线性数IC,这是由于IC与VBE之间具有对数关系的结果。在一个包含n个BJT基-射结的闭合环路中，采用某种方法使其正向偏置而导通，则结电压之和应等于零，即：

　　图1给出了一个简化TL环路，它包含4个PN结，每个PN结实际代表环路中每个BJT的基一射结，每个结上标出的电流过结的正向偏置电流，即BJT的集电极电流IC.

图1 简化TL环路

　　把式（2）代入式（3），将VBE加以替换得：

　　式中：Isj代表每个结的反向饱和电流，由于每个结的发射区面积可能不同，也可以有不同极性的BJT组成，因图简化TL环路，所以Isj可能是不相等的；Vtj代表每个结的热电压，对于大多数应用电路，可以假定所有结的热电压相等。因此，式（4）可以表示为：

　　一系列对数之和为零可以改写成一系列乘积项为1,因此式（5）可以写成：

　　为实现式（5）的环路内节点电压值和为零及IC/IS电流比的对数和为零，在维持合理的工作电流的同时，TL环路必须是成对的，那么它满足两个基本条件，即：TL环路内的结点数必须是偶数个；面向顺时针排列和面向逆时针方向排列的结数必须相等。设TL环路是对称的，满足上述两个条件，则式（6）可以另外表示为：

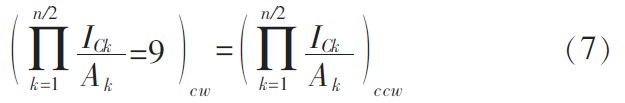
　　公式左右双方分别为顺时针和逆时针排列的正偏发射结的IC/IS项的乘积。由于TL环路中的发射结反向饱和电流ISK与发射区的面积成正比，因此可将ISK表示为：ISK=AKJSK,AK是第K个结的发射区面积，JSK是与几何结构无关的反向饱和电流密度，假设每个结JSK的是相等的，因此式（7）可以重写为：

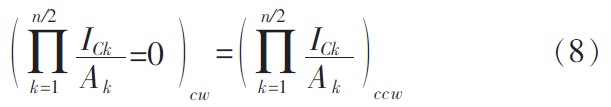
　　在跨导线性环路中，发射区面积比值很重要，通常是为了实现某些希望的性能和结果，谨慎的设计和改变发射区面积之比。当考虑TL环路中发射区面积之比时，式（8）可以表示为：

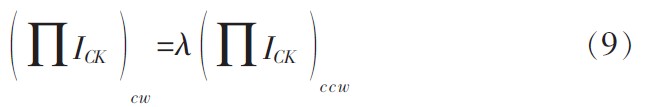
　　式（9）中λ为面积比系数。

　　当λ=1时，跨导线性原理可表示为：

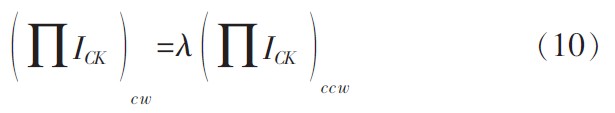
式（10）表明，在λ=1的条件下，TL环路中顺时针方向集电级电流之积等于逆时针的集电极电流之积，这是跨