基于极零点灵敏度的模拟电路可测性分析

式中：n为极点的数量；m1，m2，…，mt分别为节点1，2，…，ι的零点；c1，c2，…，ct分别为节点1，2，…，ι的直流增益；ι为电路节点的数目。

可测性可以用于指导测试节点选择。如果电路元素的数日等于极点数日和零点数目加1，就得到了最大可测性度量(所有电路元素都可识别)。如果电路有e个元件，在节点i处的可测性度量为Tt=r(r < e)，这样仅有r个元素可以识别，而e-r个元素必须假定无故障(低可测性电路)。

3 极零点灵敏度分析实例

为了描述基于极零点分析的可测性度量，作为一个例子，现给出如图1所示的3-RC梯形电路。

基于改进节点分析，电路的系统方程可以写为：

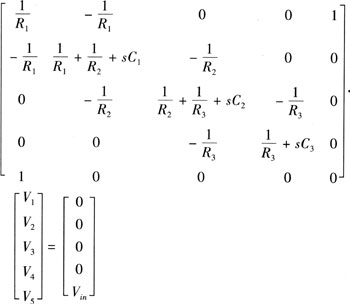
在电路节点4、节点3、节点2(V1=Vi，V4=V0)的传递函数为：

由此可以得到传递函数的极点为：p1=-1981，p2=-1 555，p3=-3 247；在节点2，传递函数的零点为：z1=-382，z2=-2 618；在节点3，传递函数的零点为：z3=-1 000。相应的极零点灵敏度见表1。

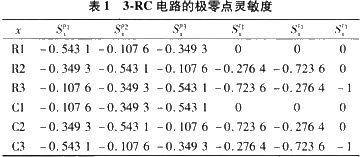
由于直流增益与元件的取值无关(电容不能短路)，因而Tk0=0。

由表1可知，Tp=3；在节点4，Tzm1=0；在节点3，Tzm2=1；在节点2，Tzm3=2。进一步分析可以发现：在节点4，Tt=3；在节点4和3处，Tt=4；在节点4和2处，Tt=5；在节点3和2处，Tt=6；在节点4、3和2处，Tt=6。也就是说，要能测试6个元素，至少必须选择节点3和2为测试点。

4 结束语

基于极零点灵敏度的可测性分析，为建立电路测试模型、确定测试点、分析测试方法提供了极大的方便。特别是当模拟和混合电路有大量的性能指标，在如何利用这些性能指标来实现测试时，显得尤为突出。