基于DSP的逆变器重复控制器的设计

O 引言

开关电源正朝着高效率、高稳定度、高功率密度、低污染、模块化发展。各种新型的拓扑电路和技术也得到了应用。谐振和软开关技术的应用也使得电源功率密度得以提高。电源控制上，控制电路、驱动电路、保护电路采用集成组件减小了电源的设计难度。高速微处理器DSP (Digital Signal Processing数字信号处理器)的出现，使得数字控制技术实时性障碍得以克服，控制采用全数字化，简化了硬件电路，提高了控制精度，也使得先进的控制方式成为可能。

比例积分控制、滑模控制和模糊控制等都是通过提高系统的动态控制特性的方法抑制干扰、改善输出波形的。这些方法对负载突变时的波形控制效果显著，但是对于周期性扰动，比如整流型负载，它们的控制效果并不理想。然而重复控制是通过对前一周期或多个周期的波形处理，利用所得到的结果对当前的控制进行校正，并且能够获得很好的波形控制效果。因此重复控制现在越来越受到人们的重视。

本文提出一种重复控制的控制方案，利用重复控制器来跟踪周期性参考指令信号，减小输出电压谐波，同时电流环控制改善系统的动态性能。并根据该控制方案，设计和调试了一台基于DSPTMS320I~F2407A控制的单相1kW逆变器，仿真和实验结果均验证了该方案的良好性能。

1 重复控制的基本理论

重复控制是基于内模原理的一种控制思想。它的内模数学模型描述的是周期性的信号，因而使得闭环控制系统能够无静差地跟踪周期信号。单一频率的正弦波是典型的周期信号，它的数学模型为

那么只要在控制器前向通道串联上与输入同频率的正弦信号，就可以实现系统的无静差跟踪。重复控制也多用数字控制方式。离散后的重复控制内模为：

式中：N为一个周期的采样次数

基于内模原理的理想重复控制系统的前向通道上含有一个周期性延时环节，不可避免它会导致动态性能较差。到目前为止，要实现高性能的控制效果，最为有效的方法有如下两种：一是直接重复控制，引入前馈，通过前馈提高动态响应，其系统结构如图1所示；二是嵌入式重复控制，它在重复控制器侧加入PI调节器，通过PI调节来提高动态性能，其系统结构如图2所示。

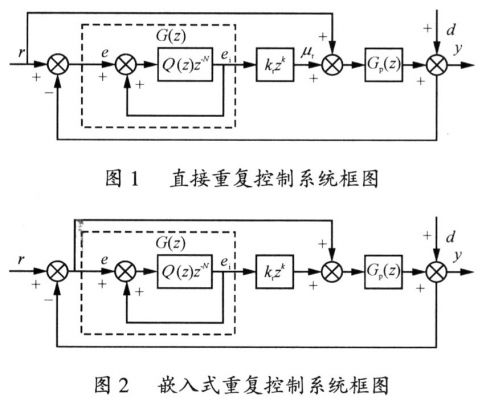
理想重复控制器Q(z)=l，当扰动的角频率ωd是输入信号角频率ωr的整数倍，即ωd=nωr时，可以得到z-N=1，就是说，理想的重复控制器可以消除任意次谐波，可以对小于采样频率的1／2下的任意次谐波进行无差跟踪。所以本文中提出的控制器通过重复内模来抑制周期性干扰，实现稳态特性，PI控制提供动态补偿，该控制器兼顾了PI经典控制设计简单，实现方便的优点，同时弥补了重复控制单周期延时的缺点。

2 逆变器控制系统设计

图3为基于DSP的逆变器系统控制方案的示意图，如果系统引入电感电流内环，不仅可以增加系统的稳定性，还能适当降低谐振峰值。因此，在重复控制电压外环的内部加入电流内环，构成重复控制双环，可以增加重复控制系统的稳定性，还能降低补偿器设计难度。

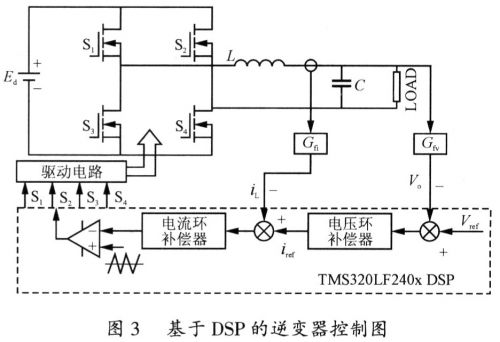
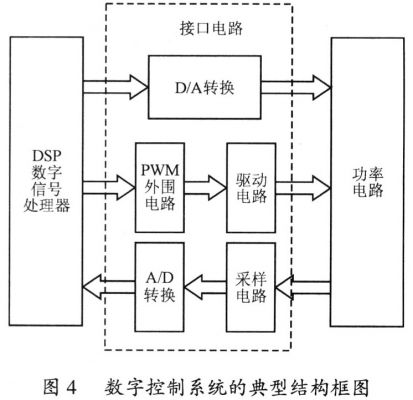
图4是数字控制系统的结构框图。系统模拟部分主要是功率电路和接口电路，数字部分。接口电路是设计时需要特别考虑的，它需要实现数据的转换(A／D，D／A)，针对不同的A／D，还需要特别设置电平转换电路。而门极驱动电路不仅要提供足够的能量以驱动功率模块，还需要隔离，以保护数字芯片。最后通过数字部分的编程，实现数字控制。

根据内模原理，重复控制设计的基础是受控系统稳定，然后加入重复内模，以获得周期性输入或干扰的无静差特性。设计重复控制系统需要知道受控系统的精确模型，这样才能设计出满足稳定域关系的补偿器。加入重复控制器后的系统如图5所示。

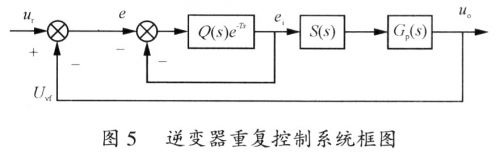
图5中T是基波周期；S(s)为需要设计的补偿器；Gp(s)为受控系统的平均模型，即式(3)。

为简化分析，忽略滤波电感等效串联电阻rL和滤波电容等效串联电阻rc，将Kvf，Utr、Ud恒定增益环节视为单位增益，可以得到简化为单位反馈的逆变器平均模型，即

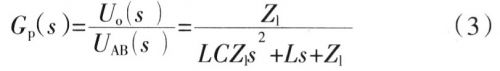
由图3可以获得重复控制系统的开环传递函数为

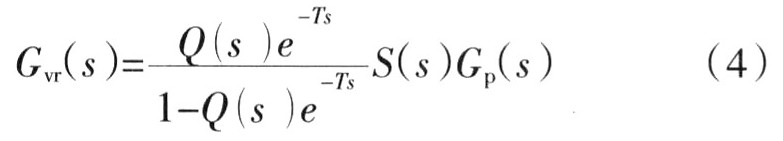
由于纯延时环节e-Ts的存在，模拟上难于实现，需要将其离散化，从而采用离散系统的分析方式。其中e-Ts=z-N，N为一个基波内的采样次数。Q是用于改善重复控制器内模临界稳定特性的，可以是一个略小于l的参数或低通滤波器，常数型Q和函数型的对比，函数型在低频段具有更高的增益，稳态特性将更加理想，不过也能看出它会引入相移，因此，需要再针对它设计相位补偿，设计不好，系统有可能不稳定，反而达不到预期的稳定性补偿效果，因此，在通常的设计中，常选择常数