基于DSP的并联电力有源滤波器的仿真研究

时间：02-08 来源：海军工程大学,电力自动化研究院作者：佚曾雨竹,吴正国,许和平点击：

1引言

近十年来，随着电力电子技术的飞速发展，电力有源滤波器(简称APF)逐步进入成熟应用的阶段。电力有源滤波器是一种基于脉宽调制、信号处理和大功率高速自关断电力电子器件的电力电子设备(不排除利用多重化技术由低频器件构成等效高频拓扑结构方式和早期的强迫换流方式)，它通过向交流电力系统实时注入与系统谐波相位相反大小相等的补偿谐波，达到消除系统谐波污染的目的。国内对电力有源滤波器的研究起步很早，所取得的理论成绩也并不比国际水平低，但是由于国民经济实力的限制，造成资金和制造技术落后以及供求关系难以形成，这一先进产品一直处于实验室阶段。

国外工程界已对有源滤波器进行了多年的实践，在电力电子设备的制造技术和运行方面积累了丰富的经验，目前已经先后有ABB、西门子、梅兰日兰等几家外国公司开始在我国国内推销该类产品。在这种情况下，推动国内电力有源滤波器的实用化研究具有迫切的现实意义。本文希望从工程应用的角度发表一些浅见。

2研究方案选择

文献[1]列举了数百篇APF的相关文献，对近年来的有源滤波器技术进行了概括性的点评。串并联合用的APF(又称UPQC)对电力系统的谐波抑制效果最佳，但成本最高，适用范围受限；串联型APF主要适合于抑制电压型谐波和扰动；并联型APF做为最基本的、也是最早出现的系统形式，主要适合于抑制电流型谐波和扰动。
文献[2]将负载产生的谐波分为电流源型和电压源型，认为并联型APF对前者有较好的补偿效果而对后者补偿效果较差，串联型APF则反之。虽然这样的分析有重要的理论意义，但是从现场的实际情况来说，文献[2]中纯粹的电容性整流型负载并不存在，即便在对蓄电池充电的场合，也会加装直流侧的平波电抗器，退一步说，即便存在这类负载，在交流侧的隔离变压器前也可使用并联型APF对负载进行补偿。因此，可以说并联型APF的适用范围要比串联型APF大得多。另外，由于工业型的三相三线制APF技术改进后即可用于民用的三相四线制情况，本文的仿真限于对工业型APF的研究，如图1所示。

图1有源滤波器示意图

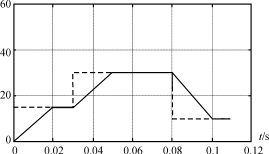
图2同步d q坐标法的阶跃响应

图3同步d q坐标法的斜坡响应

APF技术的关键在于：
（1）指令电流分离技术；
（2）补偿电流形成技术；
（3）整体系统的稳定控制。

对补偿电流的形成，目前公认的适用于较大功率场合的方法如文献[8]提供的固定频率的空间矢量脉宽调制(SVPWM)技术，只要开关频率足够高，逆变器就有足够的响应速度；对于整体系统的稳定控制策略涉及复杂的数学推导，不在本文讨论范围内；指令电流分离技术的种类繁多，而且这一部分性能的好坏直接影响APF整体性能优劣，是本文讨论的重点；另外由于近年来DSP技术的迅猛发展，使在APF设计过程中充分利用数字技术的优点并附加复杂功能的方式成为可能，因而在工程应用中用DSP实现具体算法是有意义的。

当前除直接使用模拟滤波器以外的几乎所有指令电流分离技术都可以用DSP实现，其中比较适合的方式有：瞬时虚功率法、同步dq坐标法[3]、无差拍法[4][5]和检测逆变器直流电容电压换算的方法[6]。但是瞬时虚功率法在系统电压出现畸变时不能准确检测谐波电流(见文献[9]第6章)。无差拍控制法基于零极点配置技术，对系统参数非常敏感，难以适用于实际工程应用，本身就还有待改进。检测直流电容电压的方法[6]在极端情况下将会负担一个周期的负载有功损耗[6]，因而仅适用于相对较小功率场合。同步dq坐标法对负载电流进行旋转Park变换后利用数字积分方法直接抽取对应于交流侧电气量基波成分的方法，再利用简单加减法获得补偿电流指令值，物理意义明确而且易于实现；文献[3]在同步dq坐标轴上进行积分的同时，以当前点的测量值为基准，根据坐标轴上各次谐波轨迹延伸预测下一点应产生的瞬时补偿电流，具有很明确的物理意义和工程实用性，可用于大功率场合，是本文的首选方案。

3仿真结果

本文利用MATLAB对文献[3]的方案进行了仿真研究，利用电气库对一次部分进行建模，利用SIMULINK的基本库和S函数构建具体的离散算法，并在NT工作站上进行仿真。同步dq坐标法的动态响应如图2及图3所示：(仿真频率为50Hz)

图2中，虚线为代表交流电流输入值，幅值呈两次上下阶跃变化，实线为同步dq坐标法的计算输出值，实线在第一个周期002s的上升过程是由于计算中数字积分的数组初始状态为全零值，必须经过一个周期才能精确跟上系统值的过程，这一过程会导致APF调制错误，在实际

上一篇：采用CyClockWizard软件实现系统设计和时钟管理
下一篇：硬件实时操作系统信号量管理的设计与实现

有源滤波器并联电力有源滤波器 DSP 相关文章：

栏目分类