基于DSP NNC-PID的电液位置伺服控制系统设计

2．5 外扩存储器电路

TMS320F2812将外部的存储空间映射为5个16位的区域，XINTF Zone0～XINTF Zone2、XINTF Zone 6和XINTF Zone7。其中XINTF ZoneO和XINTF Z0nel均为8 KB，并且共用片选信号；XINTF Zone2为521 KB，片选信号；XINTF Zone6为521 KB，XINTF Zone7为16 KB，共用片选信号。存储器电路使用XINTF Zone2和INTF Zone6的存储空间，选用IS6lLV25616作为存储器件。将TMS320F-2812和IS61LV25616的数据线D0～D16、地址线AO～A17、读写控制直接连接，TMS320F2812的、A18通过由逻辑门器件74AC04和74LVC32组成的译码电路后形成片选信号，从而实现了对IS61LV25616的读写控制。

3 神经网络NNC-PID控制器

神经网络是一个高度非线性的超大规模连续时间动力系统，具有大规模并行分布处理、高度的鲁棒性、自适应性和学习联想等能力，它能很好地自适环境变化，自学习修改过程参数，这些特性为神经网络应用到电液位置伺服系统控制中提供了巨大的潜力。

3．1 神经网络PID控制系统结构

神经网络PID控制系统结构如图3(a)所示。从控制系统框图中可以看出，神经网络PID控制包括两个控制子模块：NNI为被控对象模型辨识器，NNC为神经网络PID控制器。NNC-PID控制系统的工作原理是：首先获取实际被控对象的输入输出样本对，然后利用NNI对被控对象进行离线辨识，当辨识精度达到设定的要求时，通过实时调整NNC的权值系数，使系数具有自适应性，从而达到有效控制的目的。

3．2 神经网络辨识器(被控对象模型辨识器NNI)

神经网络辨识器NNI采用3层串并联BP网络实现，包括输入层、隐层、输出层，其结构如图3(b)所示。网络的输入是被控对象的输入／输出序列[u(k)，y(k)]，网络的输出为教师信号。

网络隐层的输入输出为：

3．3 神经网络NNC-PID控制器(单神经元自适应NNC-PID控制器)

由于被控对象模型不确定、不确知，并且存在着外界随机扰动，为了达到较高的控制精度，在被控对象模型离线辨识的基础上，采用单神经元自适应NNC-PID控制器结构，如图4所示。

网络的权值系数值V=[v1，v2，v3]，即表征PID控制器的3个系数KP，KI，KD。，网络的输入为X=[x1，x2，x3]，即表征3个输入参数e(k)、△e(k)、△2e(k)，网络的输出为△u(k)。

有监督的Hebb学习规则，通过对权系数的调整来实现自适应、自组织功能，控制算法和学习算法如式(10)和式(11)所示。

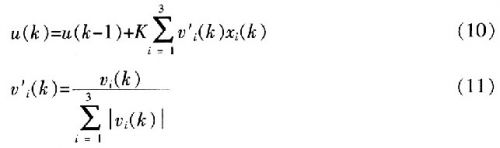
根据有监督的Hebb学习规则，权系数按式(12)～式(14)规律调整如下：

式中，K为神经元比例系数，ηI、ηP、ηD分别为积分、比例、微分的学习速率。

4 系统软件设计

系统的软件设计主要分为两部分，使用Labview编写的PC机程序和用C语言编写的DSP程序，其中PC机的程序用来显示和处理DSP发送来的数据，并向DSP发送指令及调节参数。

DSP的系统软件设计是在CCS2000的开发系统下采用C语言设计和编写，采用自顶向下的设计思路，按功能划分软件模块，系统软件如图5所示，主要由初始化模块、故障诊断、USB通信模块、机械手NNC控制学习模块和机械手NNC-PID控制模块等组成。

5 试验结果

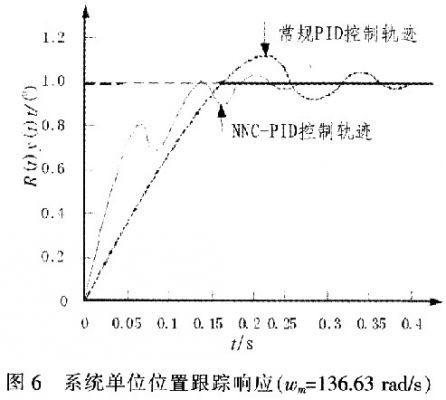
对电液位置伺服机械手系统首先采用常规的PID控制，利用Ziegler-Nichols方法整定PID参数，即控制系统在纯比例控制下，调整比例增益，使系统达剜临界稳定，记录这时的增益ku和临界振荡周期Tu，即可确定PID的参数，即：kp=0．6Tu，kI=0．5Tu，kD=0．25Tu，最后确定比例、积分、微分系数分别为：kP=1．02，kI=0．024，kD=0．006，这时系数的位置阶跃跟踪响应如图6所示。在同等情况下，采用神经网络NNC-PID控制方法对电液位置伺服机械手系统进行控制，取NNC的初始权值为PID的调定值，即：v1(0)=1．02，V2(0)=0．024，V3(0)=0．00 6，为了保证迭代的稳定性，限制权值的迭代范围：0．1≤v(1)≤1．3，0．001≤v(2)≤0．06，0．001≤v(3)≤5，这时系统的位置跟踪响应曲线如图6所示。通过对比可以看出利用神经网络NNC-PID方法，由于具有学习能力，使系统很快收敛于位置稳态值，神经网络NNC-PID控制由于能够实时调整PID参数，使系统的控制性能得到提高，同时对参数时变表现出良好的鲁棒性，很好地解决了液压系统的非线性和参数时变问题。

需要注意的是，神经元比例系数K的选择对系统的控制性能影响最重要，过大或过小都将导致系统性能变差，甚至不能实现自寻优和自适应。而ηP、ηI、ηD对系统的性能影响体现在学习速度的快慢上。

6 结束语

通过分析电液位置伺服机械手运行调试的特点及其对