可编程模拟器件在接收机动态可重构结构应用

可重构结构是一种可以根据具体运算情况重组自身资源，实现硬件结构自身优化、自我生成的计算技术。动态可重构技术可快速实现器件的逻辑重建，它的出现为处理大规模计算问题提供了一种兼具通用处理器灵活性和ASIC电路高速性的解决方案。

　　在笔者所从事的系统设计中，当模拟器件的一些性能改变但又不能及时更新调整后端的数字基带处理时，比如滤波器由于工作时间过长引起的温漂特性所带来的影响，此时就可以用可编程模拟器件替代一部分前端固定模拟器件，进而可以实时的对FPGA模块进行动态可重构操作，最终达到系统性能的最优化。

　　可编程模拟器件

　　可编程模拟器件是近年来崭露头角的一类新型集成电路。它属于模拟集成电路，即电路的输入、输出甚至内部状态均为随时间连续变化且幅值未经过量化的模拟信号;同时，该类器件又是现场可编程的，即可由用户通过改变器件的配置来获得所需的电路功能。为支持上述可编程能力，可编程模拟器件需以可编程模拟单元(CAB)和可编程互连网络(PIN)为核心，配合配置数据存储器、输入单元、输出单元或输入\输出单元等共同构成[1](见图1)。

　　

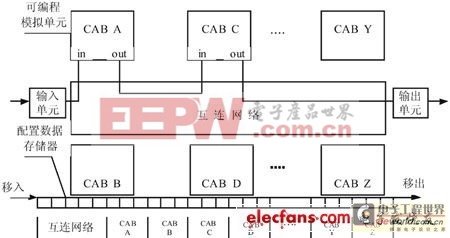
　　图1　可编程模拟器件组成框图

　　多数可编程模拟器件在单一的+5V电源电压下工作，额定功耗为100mW量级。由于采取了特殊的措施，其输入、输出线性范围通常可达到接近满电源电压量程;闭环带宽已达到数百千赫到数十兆赫;频率失真度、共模抑制比、内部噪声等指标也已达到中、高精度运算放大器的水平。

　　尽管模拟信号处理的精度低于数字信号处理方式，但仍能满足许多重要应用对计算精度的要求，而所需的电路规模较小，成本也较低。同时利用其可编程特性，还可以实现精确的自动调谐和自动增益控制，显著提高通信系统的抗干扰能力。

　　相位检测器的实现

　　TRAC(完全可重配置模拟电路)是英国FAS公司的现场可编程模拟器件系列产品的总称。它提供了一条从信号处理问题出发，可解决各种常见的信号处理问题。器件参考模拟计算机的运算单元并加以扩充，使器件内部的每个可编程模拟单元均具备加、减、取负、对数、反对数、积分、微分等8种运算功能，因此只需选定运算的类型和给出必要的参数，便可以很方便地完成对有关单元的设计，根本无须考虑单元电路的内部结构等具体细节。其内部各单元之间采取自左向右固定连接的形式，所有单元的输入\输出端均引出至器件引脚上，并且允许利用各单元均具备的“直通”和“关断”功能或者利用外接的“短路线”来修改这种基本连接[1](见图2)。

　　

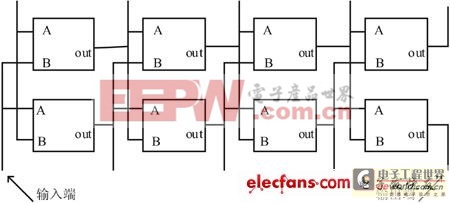
　　图2　TRAC器件结构示意图

　　在笔者所从事的认知无线电硬件平台设计中，由于需要从强信号背景环境中识别提取出微弱的信号，因而可利用TRAC器件构成相敏检测器，并将其作为锁存放大器的一部分。要实现这一目标，需要电路像窄带滤波器那样工作，除去大部分不希望要的强信号而仅允许待测的微弱信号通过。

　　图3所示为相位检测器的基本框图。输入信号和参考开关信号具有相同的频率和相位。从所示的开关输出中可望得到一个全波整流信号，而且经过低通滤波器后，便可得到和交流信号电位成比例的直流电压输出。在实际应用中，输入信号可能非常小，因此还需要加入前置放大级以支持精确的检测。因为通常需要在一定的范围内连续改变参考信号的频率，同时测量相应的直流输出。同样，若需要检测某个单一频率，则参考信号必须与待测输入信号频率相同。由于相位检测器也对相位敏感，因此当两个信号相位相同时会得到最大的输出电压。

　　

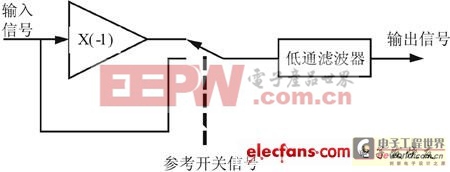
　　图3　相位检测器框图

　　相位检测器和低通滤波器一样需要利用两片TRAC器件来实现。而外部元件对于放大器和滤波器都是必不可少的，所以必须对满足条件的元件进行合理取值。

　　可编程ADC的实现

　　认知无线电接收机对其前端采用的高性能模-数转换器(ADC)及模拟器件的要求都较高，而FPGA在基带数字信号处理方面又迫切需要动态可重配置。为了适应以上要求，可以首先考虑使用可编程模拟器件来实现ADC，以下是两种具体实现方法。

　　FIPSOC混合信号片上系统

　　SIDSA公司的FIPSOC混合信号片上系统是快速开发模拟、数字集成应用的理想工具。FIPSOC芯片包括内嵌的增强型8051微处理器、现场可编程门阵列(FPGA)以及一组面向信号调理和数据采集应用的可灵活配置的模拟单元。与分离的模拟、数字FPGA方案相比，采用FIPSOC混合信号片上系统，可使产品设计周期缩短30~40%。

可编程的模拟、数字单元与8051的单片系统包括模拟单元、转换单元、可编程数字单元、8051内核和该系列中的所有器件具有兼容的存储器分布，其中转换单元含有4路DAC(分辨率可配置为8至10位)，采用逐次逼近算法，可利用