FPGA实现32阶FIR数字滤波器的硬件电路方案

　随着软件无线电的发展，对于滤波器的处理速度要求越来越高。传统的FIR滤波器一般采用通用DSP处理器，但是DSP处理器采用的是串行运算，而FPGA是现场可编程阵列，可以实现专用集成电路，另外还可以采用纯并行结构及考虑流水线结构，因此在处理速度上可以明显高于DSP处理器。本文采用并行分布式算法在FPGA上设计并实现了高速处理的32阶FIR低通滤波器，在此过程中利用Matlab的数值计算与分析功能来提高设计效率。

　　在数字信号处理中，数字滤波器的应用是极其广泛和重要的单元。与模拟滤波器相比，数字滤波器可以克服模拟滤波器所无法克服的电压漂移，温度漂移以及噪声等问题。数字滤波器根据冲击响应函数的特性，可以分为IIR滤波器和FIR滤波器两种。由于FIR滤波器只有零点、系统稳定等诸多优点。

　　1 FlR低通滤波器的窗函数实现

　　理想的滤波器频率响应中傅里叶反变换ha（n）一定是无限长的序列，而且是非因果的，而实际要设计的滤波器h（n）是有限长的，因此要用有限长来逼近无限长的，其方法就是用一个有限长度的窗口函数序列ω（n）来截取，即：

　　

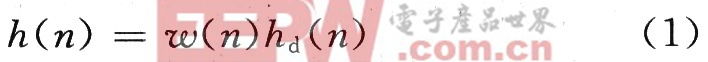
　　常见的窗函数有矩形窗、巴特利特窗、汉宁窗、哈明窗、布莱克曼窗、凯泽窗。其中，凯泽窗提供了可变的过渡带宽。本文采用凯泽窗对FIR滤波器进行设计，其窗函数表达式为：

　　

　　I0［·］为第一类变形零阶贝赛尔函数，形状参数β为依赖于滤波器阶数M的参数，用来调整主瓣宽度与旁瓣衰减，选择M可产生各种过渡带宽和接近最优的阻带衰减。给定通带截止频率ωp，阻带起始频率ωs，阻带衰减As，凯泽窗设计中有经典公式可供使用，如下：

　　

　　过渡带宽：

　　滤波器阶数：

　　形状参数：

　　

　　假设低通数字滤波器设计指标如下：

　　

　　采用上面介绍的凯泽窗，利用Matlab编程计算得到32阶FIR低通滤波器参数如下：

　　

　　32阶FIR低通滤波器幅频特性图如图1所示。

　　

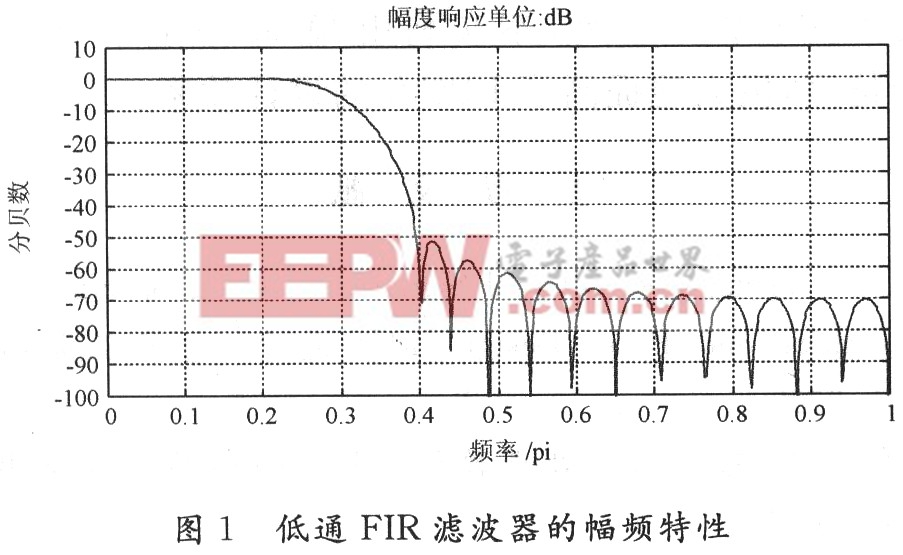
　　上述求得的系数是浮点型的，而在FPGA设计中使用的数据是定点型的，所以在设计滤波器之前要将系数转化为定点型，即系数的量化。为了兼顾精度和所占用的资源，本文的系数用12位二进制来量化，得到的整数系数结果如下：

　　

　　2 并行分布式算法原理及FPGA设计

　　32阶FIR滤波器的差分方程表达式为：

　　

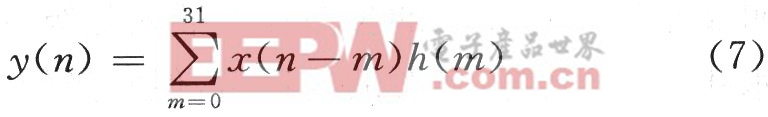
　　式中：x（n）为输入；y（n）为输出；h（n）为滤波器系数。

　　设x（n）用二进制可表示为：

　　

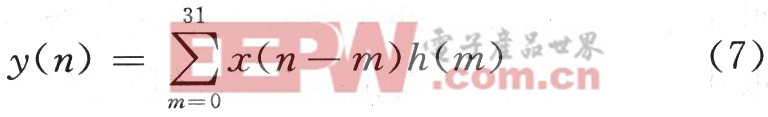
　　其中，最高位为符号位。则式（7）可写为：

　　

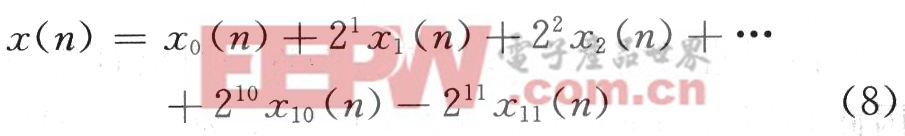
　　式（10）为并行分布式算法，由上可以看出并行分布式算法是将滤波器表达式重新排列，分别加权求和。与传统算法最大的不同之处是在FPGA设计过程中以查找表代替乘法器，即根据输入数据的不同，将对应的滤波器系数预先求和保存在ROM中，也就是将每一项的乘法求和通过并行结构查表寻值完成，提高运行速度。

　　具体FPGA实现时，首先将12位的输人数据并行输入到12列32位移位寄存器分别寄存，然后以寄存器中的值为地址，对应于查找表的结果，按照式（10），每列进行相应二次幂加权，最后各列累加，在第32个数据完全输入之后得到正确的滤波器输出。可以将32位的查找表划分为四个8位的查找表，从而降低对ROM的需求。

　　在本设计中可采用多级流水线技术，也就是将在明显制约系统速度的长路径上插入几级寄存器，虽然流水线会影响器件资源的使用量，但它降低了寄存器间的传播时延，允许维持高的系统时钟速率。

　　3 FPGA仿真与验证

　　FPGA（Field-Programmable Gate Array），即现场可编程门阵列，它是在PAL、GAL、CPLD等可编程器件的基础上进一步发展的产物。它是作为专用集成电路（ASIC）领域中的一种半定制电路而出现的，既解决了定制电路的不足，又克服了原有可编程器件门电路数有限的缺点。

　　FPGA采用了逻辑单元阵列LCA（Logic Cell Array）这样一个概念，内部包括可配置逻辑模块CLB（Configurable Logic Block）、输出输入模块IOB（Input Output Block）和内部连线（Interconnect）三个部分。 现场可编程门阵列（FPGA）是可编程器件。与传统逻辑电路和门阵列（如PAL，GAL及CPLD器件）相比，FPGA具有不同的结构，FPGA利用小型查找表（16×1RAM）来实现组合逻辑，每个查找表连接到一个D触发器的输入端，触发器再来驱动其他逻辑电路或驱动I/O，由此构成了即可实现组合逻辑功能又可实现时序逻辑功能的基本逻辑单元模块，这些模块间利用金属连线互相连接或连接到I/O模块。

　　由于直接将大量数据进行硬件仿真验证很不方便，因此利用Matlab产生一个采样频率为100 MHz，频率分别为1 MHz与30 MHz的两个正弦信号相加后，作为输入信号。vec文件，导入到QuartusⅡ中进行仿真，时序功能仿真结果如图2所示。

其中，clk为时钟信号，x_in为滤波器输入信