51单片机实现音频频谱显示的快速算法研究

1 引言

在家庭影院、卡拉OK等音响系统中，实时显示音乐信号的频谱将为音响系统增添不少色彩。目前实际生产的音响系统产品，大多采用以下两种方法实现音频频谱显示：一是利用硬件滤波器和A／D转换器；二是利用DSP处理频谱显示。前者实现简单，但硬件成本高，后者软件和硬件实现都较复杂。这里针对单片机RAM资源少、运算速度慢的特点，提出一种切实可行的快速傅里叶变换算法实现频谱显示。

2 系统整体设计及原理

该系统设计由单片机SST89V58RD2、音频数据采样电路、A/D转换电路、频谱显示电路等部分组成。图1为系统整体设计原理框图。

该系统从功能上可划分成3部分：(1)音频数据采集电路实现模拟音频信号的采样保持和量化处理，包括音频采样电路和加转换电路；(2)频谱显示电路实现模拟音频信号频谱的分段显示，它将音频信号频谱划分成14段，每段按照14级量化，由VFD显示器件显示；(3)主控制器采用SST89V58RD2单片机。在完成系统其他控制任务的前提下，充分利用单片机剩余计算资源，采用优化FFT算法计算音频信号频谱，并将计算结果输出到频谱显示电路。

3 音频信号的采集和预处理

3．1 采样频率

根据香农采样定理，一般采样频率至少应为所采样音频信号最高频率的2倍。由于人耳能够感受的频率为20 Hz~20 kHz，所以理论上采样频率最高取40 kHz。目前工业上广泛采用的采样频率大致有3种：44 kHz、16 bit的声音称作CD音质：22 kHz、16 bit的声音效果近似于立体声广播(FMStereo)，称作广播音质；11 kHz、8 bit的声音称作电话音质。本文为提高频谱计算的精度，拟采用40 kHz的采样频率和8Bit的数据位长。

3．2 样本大小

采样频率确定后，还需确定样本值，即完成一次FFT运算所需的采样点数。根据数字信号处理的基本原理，假设采样频率为Fs，采样点数为N，则FFT运算后，第n点所表示的频率为：Fn=[(n-1)×Fs]／N(1≤n≤N)。Fn若要精确到Hz，则需采样长度为(1/f)s的信号。提高频率分辨率，需增加采样点数，但这在一些实际应用中是不现实的，则采用有频率细分法，即采样比较短时间的信号，然后在后面补充一定数量的0，使其长度达到所需的点数，再作FFT，这在一定程度上能够提高频率分辨率。由于该系统是将音频信号频谱划分成14段显示，因此采用16点FFT运算，去掉第1点和第16点的结果即可。

3．3 音频数据采集电路

A/D转换器选用TLC549，它具有8位转换结果，差分基准电压输入，3线数据串行输出接口，转换时间最大达17μs，每秒访问和转换次数达到40 000次，全部非校准误差为±0．5LSB，低功耗，最大为15 mW。因此，该器件完全满足系统40kHz采样频率的要求。

图2为系统音频数据采集电路。音频信号来源于CD或DVD碟机输出的音乐信号，因而基本无噪音，考虑到音频信号是交流信号，电压范围在±0．1 V之间，而TLC549的输入必须是直流的，电压范围为0～5 V，所以还需整流和放大的预处理过程。A／D转换后得到8位数字值音频幅值的8位数字量。

4 音频频谱算法

音频频谱值的计算采用快速傅里叶算法FFT(Fast Fourier Transform)，为了提高显示器的刷新频率，系统每隔10 ms读取16次A／D转换值，得到16点实数序列，紧接着完成16点FFT运算得到16点复数序列。

4．1 倒位序及其优化算法

基2-FTT算法将原始数据倒位序存储，但运算后的结果则按正常顺序输出。原始采样数据放在数组float datalm[16]中，datalm[0]存放第1次读取的A／D转换值，datalm[1]存放第2次读取的A／D转换值，以此类推，可见第n(n=(b3b2b1b0)b)次读取的A／D转换值存放在dataIm[n]中。倒序操作后采样数据存储在float dataRe[16]中，原来第n次读取的A／D转换值存放在datalm[n](n=(b0b1b2b3)b)中。根据样本大小在系统代码段中建立倒序表数组，采用查表方式实现快速倒序操作，与移位操作等方法相比，可明显提高运算速度。

4．2 蝶形运算及其优化算法

根据基2-FFT算法，N点FFT运算可以分成log2N级，每一级都有N/2个蝶形运算，如图3所示。

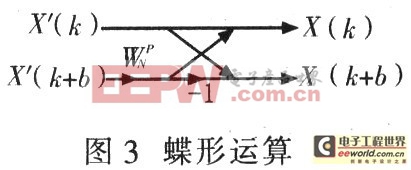
蝶形运算公式的推导过程如下：

将式(1)化简成实部和虚部的形式，得到：

可见每个蝶形运算的输出都是由其输入值与某一正弦函数和余弦函数的乘积累加得到的。由式(3)~式(6)编制正弦和余弦表，每次做蝶形运算时可查表加快运算速度。

基2-FFT算法的基本思想是用3层循环完成全部N点FFT运算：(1)最里层循环处理单独的一个蝶形运算，采用查表方法实现乘法运算；(2)中间层循环完成每一级的N／2个蝶形运算；(3)最外层循环完成log2N级蝶形运算。

由此可看出：在每一级中，最里层循环完成N／2L个蝶形运算；中间