Matlab图像增强与复原技术在SEM图像中的应用

0引 言

根据国内外的相关文献，研究和发展图像处理工具，改善图像质量是当今研究的热点。图像增强与复原是一种基本的图像处理技术。其按照特定的需要突出一幅图像中的某些信息或强化某些感兴趣的特征，将原来不清晰的图片变得清晰，使之改善图像质量和丰富信息量，提高图像的视觉效果和图像成分的清晰度，加强图像判读和识别效果的图像处理的方法。图像增强和复原的目的是对图像进行加工，以得到视觉上更好、更加容易区分的图像。

1图像处理方法

1.1 直方图均衡化

直方图均衡化(Histogran Equalization，HE)是利用直方图的统计数据进行直方图的修改，能有效地处理原始图像的直方图分布情况，使各灰度级具有均匀的概率分布，通过调整图像的灰度值的动态范围，自动地增加整个图像的对比度，以使图像具有较大的反差，大部分细节清晰。传统的直方图理论如下：

输入的直方图用H(p)表示；输入的灰度级范围为[p0，pk]，其目的是找到一个单调的像素亮度变换q=T(p)，使得输出的直方图G(q)在整个输出亮度范围[p0，pk]内是均匀的。直方图可以看作是离散的概率密度函数，变换T的单调性意味着有如下公式成立：

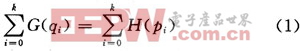
式(1)中的求和可以理解成离散概率密度函数的累积。假设图像有M行和N列个像素，则均衡化的直方图G(q)就对应均衡化的离散概率密度函数f，其函数的值是一个常数：

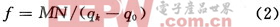
式(2)的值替换式(1)的左边，对于理想化的连续概率密度来说，就可以得到精确的均衡化直方图，这时式(1)变化为：

式(4)中的积分被称为累积的直方图，在数字图像中用求和来近似，因此结果直方图并不是理想地等同的。在离散情况下，对式(4)的连续像素亮度变换的近似为：

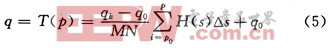
1.2频域低通滤波

对于图像这样的二维信号，经过傅里叶变换可以将其空间域转换到频率域，在频域中可以进行图像的增强操作。在分析图像信号的频率特性时，对于一幅图像，直流分量表示了图像的平均灰度；大面积的背景区域和缓慢变化部分代表了图像的低频分量，而它的边缘，细节，跳跃部分以及颗粒噪声都代表图像的高频分量。因此，在频域中对图像采用滤波器函数衰减高频信息而使低频信息畅通无阻的过程称为低通滤波。通过滤波可以去除高频分量，消除噪声，起到平滑图像去噪声的增强作用。

在频域中实现对图像的滤波过程如下：

(1)对原始输入图像进行傅里叶变换，得到频谱函数F(u，v)；

(2)利用传递函数H(u，v)对图像的频谱函数F(u，v)进行处理，得到输出G(u，v)；

(3)G(u，v)再经过傅里叶反变换，得到所希望的图像。

1.3 自适应维纳滤波

自适应维纳滤波图像复原试图利用退化现象的某种先验知识(即退化模型)，对已退化了的图像加以重建和复原，使复原的图像尽量接近源图像。图像复原的目的就是尽可能复原被退化图像的本来面目。实现图像复原需要弄清退化原因，建立相应的数学模型，并沿着图像质量降低的逆过程对图像进行复原。图像复位技术对图像退化的复原技术分为非约束复原方法、约束复原方法、非线性复原方法以及其他方法。在此，采用有约束图像复原技术中的自适应维纳滤波。该算法是用 Wiener2函数进行二维自适应去噪滤波；该函数可对一幅被加性噪声污染的灰度图进行低通滤波处理。它的运算法则是Winner2函数估计图像A中每个像素周围的局部均值和方差：

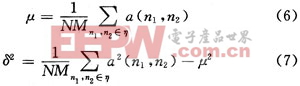
式中：N和M表示每个像素周围的N×M局部邻域。Winener2函数使用这些估计值，构建像素式维纳滤波为：

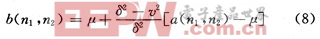
式中：v2为噪声方差，如果不指定噪声方差，Winner2函数将使用所有局部估计方差的平均值作为其参数。

2基于Matlab中的图像增强与图像复原技术在SEM图像中的应用

采用该算法对医学生物图像进行增强和复原的实现。如图1所示，原始图像的图像模糊不清，动态范围小，整个图像呈现低对比度。利用直方图均衡化处理的图像2，使整个图像的对比度明显增强，上皮细胞与周围环境的区别明显，但是图像不平滑，有噪声。经过低通滤波处理后的图3，通过滤波去除了高频分量，消除了噪声，起到了平滑图像去除噪声的增强作用，但因它去除了某些边界对应的频率分量，使得上皮细胞的边界变得有一点模糊缘效应。经过自适应维纳滤波得到的图4，很好地改善了上皮细胞的图像质量，突出了上皮细胞的整体与局部特征，达到了很好的视觉效果和区别特征。

3 结 语

所用的原始图片，是作者从事扫描电镜工作过程中所拍到并且保存的照片，细胞与背景区分不明显，无论怎么操作电镜都无法达到客户所希望的、清楚的细胞轮廓，与周围环境区别明显。图像增强可以理解为按需要进行适当的变换，对图像的某些特征，如边缘、轮廓的对比度等进行强调或