单片机中最小二乘方滤波器的向量测量和功率计算

目前，以单片机为基础的数字式电气测量、保护装置已成为主流形式。交流信号直接采样也已成为一种普通的方法。快速傅立叶算法是其中的主要算法，而最小二乘方算法，计算量很大，特别是在单片机的处理能力有限的情况下，既要保证实时性，又要保证计算速度，不经过精心设计和程序优化，很难保证二者的统一。

通过减少采样次数、使用每周滤四个采样点拟合的滤波器和一套优化措施，使该算法计算速度大大提高，可以胜任工频向量的实时测量，因而可以用于过流、速断、方向保护等多个方面。本文分析了滤波器中的向量相位关系，同时给出了以此为基础的两线制功率计算举例。该方法已通过实际应用检验。

1 最小二乘方滤波器的构造

根据文献[1～3]的研究结果，对每一路信号，输入电压函数可表示为：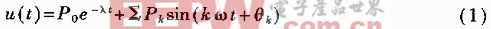

P0——直流分量值

Pk——第K次谐波分量的幅值 K=1,…，N

θk——第K次谐波的相对起始相角 K=1，…，N

ω——基波角频率，ω=2πf,f=50Hz

λ——常数，等于直流分量衰减时间常数

在一般测量、保护应用中，只关心基波成分。为减少计算量，应最大限度地减少采样次数。根据采样定理，一个正弦函数的离散采样次数量少每周波3次。为方便起见，将每周波采样次数定为4次，即采样周期为5ms。则公式（1）中只能包含直流和工频分量。将直流分量按泰勒级数展开并取其前两项，则（1）式成为：

u(t)=P0-P0λt+P1sin(ωt)cos(θ1)+P1cos(ωt)sin(θ1) (2)

其中，P0为直流分量值，P1为基波峰-峰值，θ1为基波分量在采样时刻相对于零点的相位角。

若以最近连续4次采样值为样本，可得到4个采样方程。如将P0、-P0λ、P1cos(θ1)P1sin(θ1)作为待测未知数，可将4个采样方程表示成如下矩阵：

X=A -1U (3)

其中A-1表示A的逆矩阵，亦即向量X的最小二乘方滤波器。根据文献[3]，这个滤波器为：

P1cos(θ1)=∑A-1[3][I]U[I] I=1,4 (4)

P1sin(θ1)=∑A-1[4][I]U[I] I=1,4 (5)

cos(θ1)=P1cos(θ1)/P1 (6)

sin(θ1)=P1sin(θ1)/P1 (7)

P0=∑A-1[1][I]U[I] I=1,4 (8)

P0λ=∑A-1[2][I]U[I] I=1,4 (9)

上述相量的相位关系是相量进一步运算的基础。

3 两线制功率计算

目前，高压线路的功率测量一般采用三相电压和两组电流，即两线制功率表方法。用式（4）、（5）、（6）、（7）和（10）可以实现线路有功功率和无功功率测量，具体过程如下：

两线制的前掉是假设三相电流平衡，即：

ia+ib+ic=0 (11)

如果无B相电流互感器，则B相电流：

ib=-(ia+ic) (12)

线路有功功率为：

P=Pa+Pb+Pc=ua×ia+ub×ib+uc×ic

=ua×ia-ub×(ia+ic)+uc×ic

=uab×ia+ucb×ic

=Uab×Ia×cos(θuab-θia)+Ucb×Ic×cos(θucb-θic) (13)

根据三角函数公式：

cos(θuab-θia)=con(θuab)×cos(θia)+sin(θuab)×sin(θia) (14)

cos(θucb-θic)=cos(θucb)×cos(θic)+sin(θucb)×sin(θic) (15)

其中，uab为A相和B相之间的线电压；ucb为C相和B相之间的线电压。

将（6）和（7）式结果带和（14）、（15）和（13）式，即测得三相平衡线路的有功功率。

如果输入电压是相电压，则：

P=Pa+Pb+Pc=ua×ia+ub×ib+uc×ic

=ua×ia-ub×(ia+ic)+uc×ic

=Ua×Ia×cos(θua-θia)-Ub×Ia×cos(θub-θia)

-Ub×Ic×cos(θub-θic)+Uc×Ic×cos(θuc-θic) （16）

将上式中的余弦函数展开后，再钭（6）和（7）式的对应结果分别代入即可。

无功功率的计算只需将（14）、（15）和（16）式中的余弦运算改为相应的正弦运算即可。

4 基于单片机应用的优化措施

从目前市场情况来看，虽然单片机性能在不断提高，如INTEL单片机从8位、16位到32位不断推陈出新，但真正得以广泛采用的并不是性能最好的产品。从实际应用来看，有时必须面对一个受限制的客观现实。就本应用来说，采用以下措施可大大提高程序的计算速度。

4.1 变浮点运算为整数运算

对于（4）～（10）式来说，采用C或PL/M高级语言进行浮点运算既方便，精度又高。但与整数运算相比，浮点运算速度要慢得多。因此，为提高计算速度，应尽量采用整数运算。从工程实际来看，A/D转换后的结果一般是双字节整数，可与放大10位的最小二乘滤波器直接运算，则（4）式变为：

X[3]=5×U[2]-10×U[3]+5×U[4] (17)

(5) 式变为：

X[4]=5×U[1]-10×U[2]+5×U[3] (18)

(17)、（18）式只有6次4字节的长整数乘法和4次加法。即使对12位A/D而言，（17）、（18）式的计算结果也不会溢出。由于滤波器扩大10倍时是整数，没有四舍五入，因此计算过程无任何附加误差。

4.2 快速求平方根法

从（4）～