分数阶Fourier变换应用于水声通信及其FPGA实现
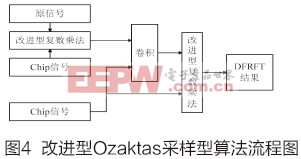
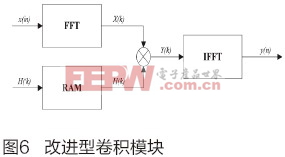
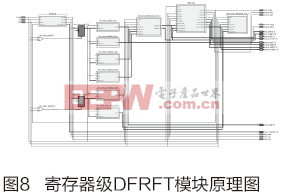
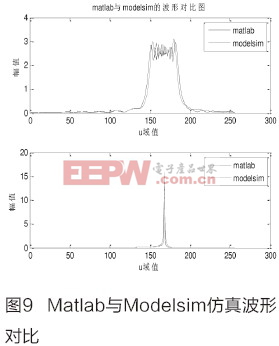
改进型算法参数如下:带宽1.0kHz,脉宽0.02s,信号中心频率分别为4.5kHz、5.5kHz、6.5kHz和7.5kHz,采样频率为48kHz。通过大数统计得到其误码率曲线如图3所示。 由图3可以知:当信噪比大于-11dB之后,4FSK调制解调方式误码率变化相对缓慢,而基于FRFT的u域调制解调方法误码率显著下降。在信噪比为-4dB时,后者的误码率接近于零。 基于Ozaktas采样型算法DFRFT的FPGA实现 基于FPGA硬件平台的改进型Ozaktas采样型算法实现流程主要分为以下两个功能模块:复数乘法器模块、卷积处理模块,其总体流程图如图4所示。 离散分数阶Fourier变换(DFRFT)计算需经过两次复数乘法运算和一次与Chirp信号的卷积运算来得到DFRFT的结果。计算结果通过峰值位置搜索判决找到其峰值点进而判断出其相对应的调频率和中心频率。 为了便于硬件的实现,减少FPGA的资源消耗,本文对复数乘法的实现进行了改进,下面具体介绍主要模块的实现过程。 改进复数乘法器模块 由图4可知本算法的实现需要两次复数乘法运算环节,因此对复数乘法的改进可提高运算效率。一般执行一次复数乘法需要4个乘法器和2个加法和减法器。本文通过代数方法重新推导公式,将复数乘法表达式重新写成另外一种只需3个乘法器、3个加法器和2个减法器的表达式。设A=Ar+jAi,B=Br+jBi是两个复数,那么复数乘法的标准表达式如下: R=A×B=(Ar+jAi)×(Br+jBi)=Rr+jRi (3) 其中Rr=Ar×Br-Ai×Bi,Ri=Ar×Bi+Ai×Br,上述标准表达式需要使用4个乘法器。通过代数方法重新推导整理为: Rr=Ar×Br-Ai×Bi (4) 复数结果的新表达式是: Rr=[(Ar+Ai)×(Br-Bi)]+(Ar×Bi-Ai×Br)(3次乘法) (8) 综上可知:改进的复数乘法可用3个乘法器、3个加法器和2个减法器实现。在Cyclone系列FPGA中,每个8×8位乘法器需95个逻辑单元,而每个位宽16位的加法/减法模块只需18个逻辑单元,即改进后的复数乘法器减少41个逻辑单元,降低了FPGA的资源消耗。 卷积模块 本文采用FFT运算完成卷积运算[11]。基于快速傅立叶变换的卷积计算流程如图5所示。分别对x(n)和h(n)进行FFT运算,得到对应的频域响应X(k)和H(k),将X(k)和H(k)相乘的结果再做IFFT,即可以得到x(n)和h(n)的卷积结果y(n)。 由于进行卷积的Chirp信号已知,为了降低FPGA的资源消耗,可预先计算Chirp信号的FFT结果,并将其保存到RAM中,即可减少一次FFT硬件运算。其改进快速傅立叶变换的卷积计算流程示意图如图6。 两次FFT运算共需要2×1/2Nlog2N次相乘还有N次相乘,因此共需要相乘次数为m=N(1+lbN)。传统方法直接计算线性卷积需要n=ML次乘法。当x(n)和h(n)点数相同时,则M=L,传统直接计算方法与改进方法进行卷积计算的运算量[12]比较为: 由式(10)可知M值越大,此算法的优越性越明显。用硬件语言设计出改进快速傅立叶变换的卷积部分并生成模块,如图7所示。 DFRFT模块测试 DFRFT的各个模块设计完成之后,通过顶层模块把各个模块连起来,形成一个完整的模块。其寄存器级原理图如图8所示。 为了验证该模块的正确性,将FPGA与Matlab的计算结果进行对比。利用Matlab产生Chirp信号(信号中心频率为2000Hz,调频斜率为400000,最佳阶次p=1.2)。并将其传送到FPGA的DFRFT模块。图9为FPGA输出与Matlab仿真结果的对比图,从中可知二者基本一致。当且仅当搜索阶次p为最佳阶次时,Chirp信号能量聚集为一个冲击函数,从而证明了该模块的正确性。 结论 本文初步研究了分数阶Fourier变换在水声通信中的应用,探讨了基于分数阶Fourier变换的U域调制方法。通过理论分析、仿真研究表明:该应用能够提高系统的抗噪声干扰、抗多径干扰和频率选择性衰减的能力。并在FPGA上完成了该方法的实现,验证了算法的可行性。 参考文献: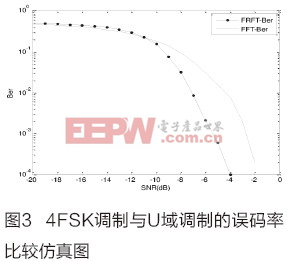 ?
? ?
?
Rr=Ar×Br-Ai×Bi+0 (5)
Rr=Ar×Br-Ai×Bi+(Ar×Bi-Ai×Br)-(Ar×Bi-Ai×Br) (6)
Rr=(Ar×Br-Ar×Bi+Ai×Br-Ai×Bi)+(Ar×Bi-Ai×Br) (7)
Ri=Ar×Bi+Ai×Br(复用来自Rr的乘积) (9)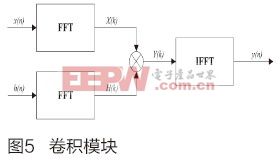 ?
? ?
?
???????? 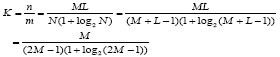 ?? (10)?
?? (10)? ?
?
 ?
?
[1] 殷敬伟.水声通信原理及信号处理技术[M].北京:国防工业出版社,2011:1-2
[2] A.V.奥本海姆,R.W.谢弗[著],董世嘉等[译].数字信号处理[M].北京:科学出版社,1981:1-3
[3] 惠俊英,生雪莉.水下声信道[M].北京:国防工业出版社,2007:1
[4] 黄晓平.水声扩频通信研究[D].哈尔滨工程大学,2006
[5] 刘榕.基于FRFT的LFM抗干扰通信研究[J].山西电子技术,2007:1
[6] 陶然,齐林,王越.分数阶Fourier变换的原理与应用[M].北京:清华大学出版社,2004:1-150
[7] S.C.Pei,J.J.Ding.Closed Form Discrete Fractional and Affine Fourier Transform[J].IEEE Trans Signal Processing,2000,48,(5):1338-1353
??? [8] V. Bargmann.On a Hilbert Space Of Analytic Functions and an Associated IntegralTransform[J],PartI.Comm.Pure.Appl.Math,1961:187-214
[9] 赵兴浩,陶然,邓兵,王越.分数阶Fourier变换的快速计算新方法[J].电子学报,2007,35,(6)
[10] 郭斌.分数阶Fourier变换的基本原理与应用[D].电子科技大学,2006
[11] 范海波.基于FPGA的线性卷积的实时实现[J].电子科技,2010,(5)
[12] 焦瑞莉.数字信号处理[M].北京:机械工业出版社,2011:125-200
Fourier FPGA 水声通信 201307 相关文章:
- 在采用FPGA设计DSP系统中仿真的重要性 (06-21)
- 基于 DSP Builder的FIR滤波器的设计与实现(06-21)
- 基于FPGA的快速并行FFT及其在空间太阳望远镜图像锁定系统中的应用(06-21)
- 3DES算法的FPGA高速实现(06-21)
- 用FPGA实现FFT算法(06-21)
- FPGA的DSP性能揭秘(06-16)
