基于DSP的图像压缩系统设计

I1

O1=I0-I1

需要2次加法完成，倍乘因子的输入/输出关系比较简单：,只需1次乘法，旋转因子的运算关系为：

需4次乘法、2次加法完成。如果对其输入/输出关系式做以下变换：

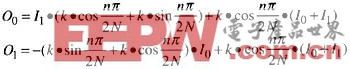
只需要3次乘法、3次加法。其中，

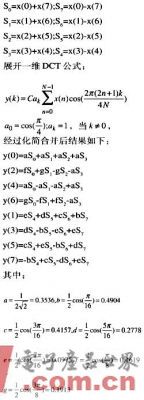
和差都是已知系数，可通过查表获得。

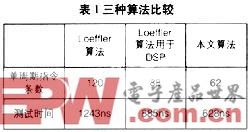
由此计算可知，一个8点DCT的Loeffler算法共需要11次乘法和29次加法。从DSP汇编语言编程的角度来看，一个代数运算应包括取操作数、运算、存操作数三个步骤。因此，该算法大约需要120条指令。C5409的运算能力很强，支持单周期加/减法和单周期乘法运算，并且能够在单周期内完成两个16位数的加/减法运算，再加上DSP中有3组数据总线，因而可以利用长操作数(32位)进行长字运算。在长字指令中，给出的地址存取的总是高16位操作数，因而只需5条长字指令即可计算2个蝶形运算。加上采取其它优化措施，大约需90条指令完成Loeffler算法。

虽然Loeffler算法运算量最小，但是运用于本文系统并不是最优。因为该算法是为高级语言设计，没有利用汇编语言的特点和DSP硬件的特点。本文提出了基于DSP乘法累加单元的DCT快速算法。

DSP的乘法累加单元能在单周期内完成一次乘法和一次累加运算。如汇编指令运用于DCT运算，将大大简化程序的复杂度并减少计算时间。具体算法如下，利用蝶形运算：

从上面表达式可以看出，y(0)-y(7)都是乘法累加运算，而s0-s7可由x(0)一x(7)经过蝶形运算得到，因此，DCT算法由原来的4级运算变成两级，即第一级蝶形运算和第二级乘法累加运算，第一级蝶形运算共要10+4=14(10次计算操作和4次辅助操作)条指令，第二级运算中，每个输出要4+1+1=6条指令(做4次乘法累加运算、1次读取操作和1次存储操作)，一共48条指令，这样，计算一个8点DCT要62条指令，大大缩减了运算时间，提高了CPU的工作效率，增强系统的实时性。

量化运算优化

本文提出了基于实际情况的自适应量化方法，即量化阶段采用二次计算的方法，其算法主要分为两步：(1)对变换后的图像系数进行自适应处理;(2)构造新的量化表。具体方法如下：

首先求出亮度分量和两个色度分量在频域中所有8×8子块的63个交流系数绝对值的平均值P(u,v)，其中，u,v=0…7为位置信息。接下来求出163个交流系数平均值中的最大值，Z1(u,v)=MAX[P1(u,v)],最后将63个交流系数平均值进行归一化处理，同时加入频率位置信息，分别得出亮度和色度量化表中63个交流分量的矫正系数，计算过程为：

由此可以得到量化表的矫正式Qpl(u,v)=Q1(u,v)/X1(u,v)，对JPEG量化表进行矫正。

将上述矫正后的量化表作为最终的量化表，对图像进行标准JPEG压缩，形成完全符合JPEG格式的压缩文件。本算法的解码过程与标准。JPEG解码过程完全相同，可以看出它也是标准。IPEG编码过程的逆过程。

实验结果

快速DCT运算

将本文提出的算法、Loeffler的DSP优化算法和纯Loeffler算法分别进行测试。结果见表1,可以看到本文算法较Loeffler的DSP优化算法大约节省了1/4的时间，较纯Loeffler算法大约节省了一半时间，其效果是十分明显的。

自适应量化

对自适应量化器进行仿真。本文采用中等复杂度的标准图像作为测试图，与基本JPEG系统进行性能比较(基于峰值信噪比(PSNR))。只将JPEG标准方法中的量化表更改为修正的量化表，就可以在同等压缩比下，提高恢复图像的质量。表2为不同压缩比下，采用JPEG量化表和自适应量化表两种方法的峰值信噪比。从压缩比和峰值信噪比的对比结果可看出，自适应量化JPEG方法的压缩比略高于标准JPEG方法。

结语

该系统的优点是提高了JPEG的运行速度，增强了图像的压缩率和质量，并且易于硬件实现。这一方案可应用于需要对视频图像进行实时采集、压缩及存储的绝大部分场合。