DC-DC buck变换器的混沌现象分析及其控制

自从Hamill等人报道了关于电力电子电路中出现分岔与混沌现象以来，对在工业中有着广泛应用的DC—DC开关功率变换器中复杂行为的研究引起了业内关注，并取得了一些有意义的成果。Aroudi等人系统阐述了DC—DC开关功率变换器非线性动力学行为及建模方法的研究进展，并研究了DC—DC开关功率变换器的分岔现象及其控制;张波则在对DC—DC功率变换器非线性现象的基本类型进行分析和综合的基础上，指出了DC—DC开关功率变换器混沌研究的发展方向以及未来的应用前景。众所周知，在实际应用中，通常要求DC—DC开关功率变换器工作在稳定的周期1状态。然而由于温度、元件老化、外部环境的变化以及其它干扰因素等影响，使系统的工作状态发生变化而不能保持系统原有性能，从而无法达到预期目的，特别是当系统运行于混沌状态时，混沌的不确定性将导致系统的运行状态无法预测，从而使功率变换器的控制性能受到较大影响，甚至完全无法工作。因此，研究如何实现对该电路系统中的混沌进行有效控制具有重要的应用价值。迄今为止，已有多种方法成功地应用于DC—DC开关功率变换器中，实现了混沌控制。例如，滑模变结构控制、脉冲电压微分反馈控制、参数微扰控制、自适应控制、Washout滤波器控制、延时反馈控制等，为实际工程设计奠定了理论基础。

本文从系统能量的角度分析了电压反馈型DC—DC buck变换器的混沌产生机理，指出随着输入电压的增加，系统的平均能量也随之增加，当系统平均能量超过某个极限值时，将会发生系统平均能量的急剧增加，从而导致系统产生混沌。同时还指出，系统稳定于周期nT状态，是因在nT周期内，系统只是把从电源处吸收的能量，毫无保留地传递给负载，即系统在这nT周期内的外在表现，只起一个能量传递的作用。在此基础上，以电感电流为控制变量，设计了一个脉冲反馈控制器来控制DC—DC buck变换器中的混沌行为，并给出数值仿真结果，另外基于Pspice电路仿真软件，设计出电压反馈型DC—DC buck变换器电路及控制电路，从电路仿真角度进一步证实了控制方法的正确性和有效性。

1 DC-DC buck变换器的分岔与混沌现象

PWM型电压反馈型DC—DC buck变换器的电路原理如图1所示。假设电路中所有的元件均理想，即比较器的增益无穷大，开关S的导通电阻为零，断开时的电阻无穷大，同时，开关没有延迟。当开关S导通时，输入电压向负载和电感提供能量，而当S断开时，电感电流将通过二极管将电感中存储的部分能量提供给负载。

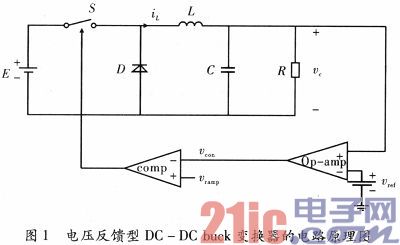
假设运算放大器工作在线性区域，其增益为a，则

因此，当vramp>vcon时，比较器输出高电平，开关S导通，二极管D截止;当vramp

电路参数选取如下：L=20 mH，C=47μF，R=22 Ω，vref=11.3 V，VL=3.8 V，VH=8.2 V，T=400μs。采用Matlab/Simulink进行仿真，步长为4×10-6s，可得其以输入电压为分岔参数的能量W的分岔图，如图2所示，当20 V≤E33.5 V时，系统所具有的能量随着输入电压的增加而增加，但没有跳跃现象发生，因此，系统处于稳定状态。当E=33.5 V时，系统所具有的能量则急剧增加，从而导致系统混沌的产生，而当E>33.5 V时，系统的能量则一直处于跳跃状态，能量大时、小时，因此，系统所具有能量的增加是系统产生混沌的主要原因，即，当系统所具有的能量超过某一个极限值时，混沌现象将发生。但仅从图2则无法得出系统以何种途径达到混沌状态，因此，还应考察系统在nT周期内，系统所存储的能量，如果存储的能量等于零，则说明系统在这nT周期内只是起能量传递的作用，即把输入的能量全部传递给负载。此时，系统则稳定于周期nT状态。例如，当n=1，2，4，8时，能量W1以输入电压为分岔参数的分岔图分别如图3(a)～图3(d)所示。在一个周期内，如果在开关断开期间，能将开关闭合期间电源给电感和电容提供的能量，全部传递给负载，则系统处于周期1状态，如图3(a)所示。当E∈(20 V，24.7 V)，系统稳定于周期1状态。例如当E=23 V，系统的相图如图4(a)所示。在两个周期内，如果在开关断开期间，能将开关闭合期间电源给电感和电容提供的能量全部传递给负载，则系统处于周期2状态，如图3(b)所示。除去周期1部分，即当E∈(24.7 V，32.2 V)，系统稳定于周期2状态。当E=28 V，系统的相图如图4(b)所示。同理，可以分析当E∈(32.2 V，33.1 V)，系统处于周期4状态。当E=32.5 V，系统的相图如图4(c)所示;当E∈(33.1 V，33.5 V)，系统处于周期8状