一种混沌组合序列密码电路设计与复杂度分析方法

1 引言

在密码学领域，利用密码技术|0">密码技术对传输信息进行加密发送、解密接收，是一种行之有效的方法。密码学发展至今已有许多优秀的算法发明并得到应用，例如私钥密码体制中的DES密码、IDEA密码、序列密码；公钥密码体制中的RSA密码、椭圆曲线密码等，他们各有设计特点和对应的应用领域，其中序列密码一直是密码学中最重要的加密方式之一。利用组合LFSR序列作为序列密码的前馈电路，可充分利用m序列的良好统计特性和加大输出序列周期和线性复杂度的优势，但如何在保证前馈电路输出统计特性不被破坏的基础上，置换与混乱输出关系，增强密码的保密性仍是该领域研究必须思考的问题。传统方法是利用非线性函数对前馈电路输出进行变换，但在函数设计与生成速度上制约了其发展；利用某LFSR序列产生控制信号去控制并行LFSR序列，这种形式电路如Geffe发生器、Jenning发生器、交错停走式发生器等，易受到相关性攻击，应避免在保密强度要求高的部门应用。随着现代科学技术的发展，将神经网络、混沌等算法融入密码学的研究已不断深入，伴随着数字化技术和大规模集成电路的快速发展，一些算法不仅停止在理论研究与模拟仿真实验上，利用硬件电路进行设计并实现已逐渐成为事实。如何衡量加密芯片的复杂度是应该研究的问题，当加密芯片被敌方得到并破译时，以高复杂度保持加密信息的安全性是加密芯片成功设计的关键。现提出一种混沌组合序列密码复杂度分析与设计方法，并由此设计混沌组合序列密码电路并基于FPGA实现。

2 序列密码原理

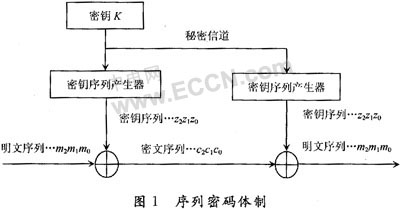
由于语音、图像和数据等信息都可以经过量化编码转化为二进制数字序列或本身就是二进制数字的序列，因而可以假定序列密码系统中的明文为二进制数字序列组成的集合m={mi}，密钥空间为K，密文空间为C={ci}。如图1所示，对于每一个k∈K，由算法Z可以确定一个二进制序列Z(k)=z0，z1，z2，…，当明文为m0，m1，m2，…，mn-1时，在密钥k下的加密过程为：对i=1，2，3，…，n-1，计算ci=mi○+zi，密文为c=Ek(m)=c0，c1，c2，…，cn-1，对密文c的解密过程是：对i=1，2，3，…，n-1，计算mi=ci○+zi，由此恢复明文为m。通常，称密钥k为种子密钥，由k通过算法Z产生的序列Z(k)称为密钥序列。

由此可见，序列密码的安全性主要取决于密钥序列Z(k)和序列密码算法的难破译性。当z0，z1，z2，…为均匀分布的二进制随机序列时，则该密码系统为一次一密系统，因此是不可破的。但是由于Z(k)是一个由k通过确定性算法产生的伪随机序列，所以该密码系统的保密性关键是高复杂度设计。

3 密码芯片电路设计

根据国内外在混沌序列密码研究的分析，本文设计了基于FPGA的混沌序列密码芯片，该芯片核心部分是混沌序列密码模块，如图2所示。加密芯片除混沌序列密码模块外还有控制模块和加／解密传输模块。

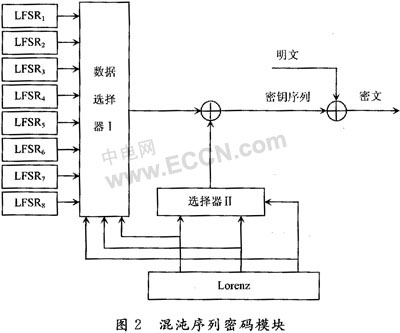
从该框图可以看出，由8个LFSR序列作为驱动源，Lorenz混沌系统与数据选择器Ⅰ构成对8个LFSR序列进行非线性变换部分，数据选择器工输出序列与数据选择器Ⅱ输出序列相异或后产生密钥输出序列。

选择器根据Lorenz混沌系统选择信号输出，其中选择器的控制端信号也来源于Lorenz混沌系统的任意一输出。根据多个LFSR序列作为驱动源的特性得知，当LFSRi(i=1，2，…，n)的级数N1，N2，…，Nn两两互素且满足一定条件时，该组合序列输出周期为。为了使输出序列有尽可能大的线性复杂度，各Ni应尽可能接近N／n，其中N=N1+N2+…+Nn。当Ni确定以后，为使每个LFSRi(i=1，2，…，n)生成周期为2Ni-1的m序列，其充要条件是使其特征多项式为本原多项式。

4 密码芯片电路的复杂度分析

该结构输出周期较单一LFSR作为前馈电路的输出周期大大增加，同时此电路的复杂度大大增加，可从以下证明中得到。

该密码电路中构成线性复杂度的主要器件有8个LFSR、混沌序列发生器及数据选择器，设8个LFSR级数分别为Di(i=1，2，…，8)且互不相等，di(i=1，2，…，8)分别为8个LFSR的输出，a0a1a2为Lorenz混沌序列输出，设Y1(t)，Y2(t)分别为数据选择器Ⅰ和Ⅱ的输出，那么：

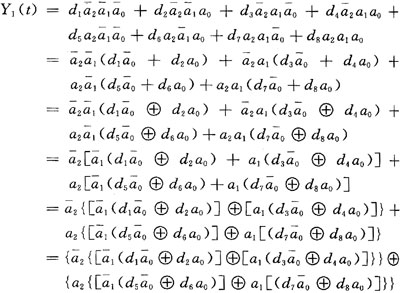
如果假设混沌每个输出序列复杂度为A，LFSR的复杂度分别以他们各自级数表示，依据复杂特性基本定理，则Y1(t)的线性复杂度L1可由上面的逻辑输出表达式计算为：

此式给出描述多控制端的数据选择器线性复杂度的基本公式，可看出该电路线性复杂度主要由An项决定，如果LFSR数目增加，复杂度将为幂指数增长。

5 加密芯片电路输出测试

利用ALTERA公司的QuartusⅡ工具和目标芯片EP20K300EQC240设计，对逻辑综合结果进行仿真后完成硬件下载功能。为验证其输出序列的平衡性、相关性及游程等特性，对下载后输出序列利用Agilent1693A逻辑分析仪进行数据测试、存储并利用Matlab进行统计分析。在实际应用中，如果平稳随机序列满足各态历经性，统计均值可用时间均值代替。取一个有限的计算系统能够承受的时间均值和时间自相关序列，并用他们作为统计均值和统计自相关序列的估值。根据此理论设定一初始数据，在一段时间内观测其输出序列的平衡性、游程性、自相关性及互相关性，基本满足密码序列输出要求，现以自相关特性测试为例进行说明。

将混沌组台序列转化成X={x(n)|n=0，1，2，…，x(n)∈{-1，1}}，使序列输出概率密度关于0对称。取测试序列N=12×104，并利用自相关函数的估值式(5)进行仿真，得到该神经网络序列的自相关特性如图3所示。可看出该密码序列输出具有较好的自相关特性，在0值处峰值尖锐，其他值近似为0，类似于δ函数。