轻松实现3D图形处理的设计技巧

源的角度，物体与光源的距离，人眼与物体的角度、距离等因素来计算最终的光照强度。

光源主要包括平行光、点光、聚光。物体对光的反应特性主要包括反射、吸收、透射。其中最主要的反射，包括环境泛光、漫反射、镜面反射。泛光主要用来体现环境中物体散射到物体并反射的光。漫反射是物体向空间各角度均匀反射的光，其强度与入射角的余弦成正比，但与视点无关。镜面反射是朝特定方向反射的光。当镜面反射光恰好进入视点时，将能看到通常所说的高光面。

3.1.3 可见性判断

3D场景绘制，是对真实情况的建模和显示，物体之间严格按照自然的遮挡关系，物体每个点在视野中的前后都需要经过判断，以确保近处的能恰当得遮挡远处的。因此需要设定专门的深度缓存，屏幕上的每个像素在绘制前都需要根据深度来判断，如果前面有不透明物体遮挡的话，该点将不会被绘制。

另一方面，对于不透明的封闭几何体，背朝视点的面不需要显示，将可以直接于早期剔除，出现在视椎体边界的三角形需要进行裁剪，形成新的三角形。

3.1.4 扫描光栅

3D图形绘制流程中，如果对物体的每个像素都做坐标变换或是光照计算等操作，将会导致庞大的计算量，因此在采用三角形拟合物体的算法中，往往仅计算三角形顶点的这些属性，三角形中的点，就又顶点的属性插值而成，由于这项工作将面向每个三角形中的每个像素，运算过程中将需要访问颜色缓存与深度缓存还有纹理贴图数据。这些导致该过程的计算量占图形处理的大部分。如何高效地插值填充三角形内的像素，将显著影响3D图形性能。

扫描光栅算法中，一系列像素是紧挨着的，因此为递推算法和Cache命中提供了天然了方便，然而如何在特定的软硬件平台下充分利用这些特性来取得高性能，需要细致研究。

3.1.5 纹理贴图

物体的纹理包括表现其表面光学属性的颜色纹理，以及表现其表面围观几何形状的几何纹理。纹理主要使用图像、函数或其他数据来改变物体表面的外观细节。很多时候，物体的细节并不需要通过几何建模来精确实现，采用纹理贴图的方式能快速高且真实感地实现这一点。但纹理的使用包含多个关键技术。坐标经过透视变换后，物体各个像素的属性与屏幕坐标之间就不再是线性的关系，由于扫描光栅过程中，三角形中像素的纹理坐标是通过插值得出的，在透视变换后，这种插值的结果将产生失真，需要特定算法进行矫正。为了防止纹理采样时的混叠现象发生，纹理采样通常需要进行多点采样并滤波得出最终结果。为了提高效率，当物体离观察者越近越大时，采用高分辨率的纹理图像，而越远越小时，则采用低分辨率的纹理图像。

3.2 图形绘制系统硬件结构

3D图形处理领域早期采用全硬件的电路来依次实现图形绘制流水线中的各个阶段。尽管全硬件的结构使得性能和效率都非常高，但灵活性则大大损失。即使在同一个硬件平台上，不同的应用程序，不同的3D场景，都有各自不同的特点。绘制这些不同的场景，通常在不同的阶段有不同的负荷，有时需要采用不同侧重的算法。这些都是固定结构硬件无法实现的。

随着半导体工艺的进步，同样的面积和功耗下，能够实现更多更复杂的系统。因此，基于可编程处理器的3D图形绘制系统被广泛采用，通过编写程序来实现3D绘制中的许多功能，这虽然牺牲了一些性能，但在灵活性上换回得效果使这种方案更具性价比。但特定的算法，例如纹理滤波、颜色混合等计算任务的硬件性能高出软件许多倍，因此仍保留使用硬件实现。

本课题组采用这种可编程处理器，配合固定功能硬件的架构来实现3D图形系统。

3.2.1 顶层结构

图3.2.1 图形处理器系统顶层

3D图形处理器包含一个可编程的顶点处理器及一个基于Tile绘制方法的光栅单元。为保留采用多个图形处理器的方案，系统采用基于SOPC的Nios嵌入式软核作为整个系统的控制中枢，与1到多个图形处理器构成异构片上多核系统，对以后可能将实现的指令发射，控制计算解耦合等技术留下空间。单个图形处理器中除了顶点处理器及光栅器外还包含一个总线接口、一个DMA、一个DDR2控制器、一个指令Cache和一个纹理Cache。系统的外围，包括VGA控制器，用户输入等人机交互接口和Flash控制器，风扇控制器，测温控制器等外设IO。

3.2.2 顶点处理器结构

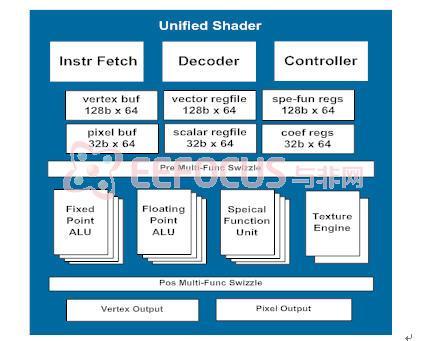
图3.2.2 可编程顶点处理器结构

面向移动设备的3D图形处理器对效率的苛求远远大于桌面系统，目前许多商用嵌入式图形处理器IP都直接采用片上指令存储器，对于指令的效率相当敏感。本设计没有采用高位宽的指令集，而是将指令格式控制在32位。并通过设置特殊状态寄存器来辅助指令实现更灵活更丰富的操作，包括操作数