IIR数字滤波器的FPGA仿真与实现

数字滤波器是实现数字滤波的核心器件。常用的数字滤波器有FIR数字滤波器和IIR数字滤波器。文章介绍了一种基于EDA技术中的模块化设计思想，采用VHDL硬件描述语言对IIR数字滤波器中的一些关键电路模块进行设计,最终在FPGA上实现IIR 数字滤波器的方法[1]。

1 IIR数字滤波器硬件设计原理

1.1 数字滤波器的原理

数字滤波器的功能是完成信号滤波处理，是用有限精度算法实现离散时间线性非时变系统[2]。一个数字滤波器的系统函数H(z)可以表示为：
　　

直接由H(z)得出表示输入输出关系的常系数线性差分方程为：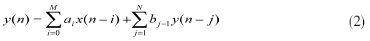


式中ai、bj-1为滤波系数，当bj-1均为零时，该滤波器为FIR数字滤波器，当bj-1不均为零时，则为IIR数字滤波器。

1.2 IIR数字滤波器的硬件实现方案比较

滤波器的实现主要包括两大类：采用TMS320系列DSP芯片实现和采用PLD器件实现(主要包括FPGA和CPLD)。利用PLD器件实现时，可以采用硬件乘加模块，从而使其运算速度比采用DSP器件快很多。因此基于FPGA的自编程实现方式成了滤波器实现的首选[3]。以下简要介绍IIR数字滤波器的设计方案和基于FPGA的实现方法[4]。

方案一：直接相乘累加式

对于二阶的IIR数字滤波器，其差分方程为：

因此可用5个硬件乘法器和4个硬件加法器来实现，采用这种方法对于高阶的IIR数字滤波器的FPGA的设计来说是比较耗费资源的。

方案二：基于ROM查找表的VHDL结构化设计[5]

滤波器实现的主要任务是完成乘累加运算，采用ROM查找表方法可以避免使用硬件乘法器。由二阶IIR滤波器的差分方程可以看出：yn仅取决于变量xn、xn-1、xn-2、yn-1和yn-2，因此可将a0、a1、a2、b0、b1的所有部分积存储在ROM中，而以变量xn、xn-1、xn-2、yn-1和yn-2作为ROM的地址，从中选出对应的值，从而得到yn。

此方法避免了占主要运算量的乘法运算，节省了FPGA硬件资源，但使用不够灵活。特别是当阶数比较大时，更改ROM内的数据十分不便。

方案三：改进型设计

结合直接相乘累加式和ROM查表法的优点，用1个5路8位×1位的乘法器在8个时钟周期内实现。其实现结构如图1所示。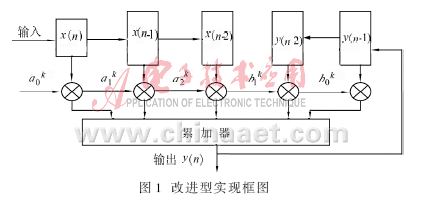

图1中的X(n)与各自的系数的最高位相乘后，送入累加器相加后将和左移一位，以实现乘2运算。下一个时钟，寄存器内数据与系数的次高位相乘，再送入累加器，然后再左移一位。接下来的6个时钟进行类似的操作。第8个时钟后，将累加器所得数据输出即得到y(n)，对累加器清零，接着再进行下一次运算。

比较3种方案，方案三实现较为方便简洁，在节省了FPGA硬件资源的同时，使得设计灵活，设计周期大为缩短，本设计即采用方案三来实现IIR数字滤波器。

2 IIR数字滤波器的具体实现和仿真

二阶级联法用于实现IIR数字滤波器硬件电路的应用是极为广泛的，为此本文首先实现数字滤波器的二阶节，然后用二阶节的级联实现更高阶的滤波器。

2.1 IIR数字滤波器二阶节的FPGA实现

IIR数字滤波器的二阶节电路采用模块化设计，把二阶节分为延时模块和补码乘加模块，其中补码乘加模块是设计的核心。

2.1.1 延迟模块

延迟模块功能是在clk时钟作用下将差分方程的各x、y值延迟一个时钟以实现一次延时运算，即当延时模块输入为x(n)和y(n)时，经过延时后输出x(n)、x(n-1)、x(n-2)、y(n-1)和y(n-2) ,然后将输出送到补码乘加模块运算。

2.1.2 补码乘加模块

补码乘加模块主要是用方案三的方法实现输入序列{x(n)}、{y(n)}与系数ai、bi分别相乘后再相加的过程，即实现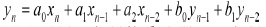。为了避免过多地使用乘法器，本设计中乘加单元(MAC)的乘法器采用阵列乘法器，以提高运算速度。

2.1.3 二阶节的顶层模块设计

顶层模块设计采用原理图输入方法，将延迟模块和补码乘加模块加入到系统中，并加入相应的输入输出引脚构成IIR滤波器的二阶节。

2.1.4 二阶节的系统仿真与结果分析

本次设计的二阶节的输入端x(n)宽为8位，可接8位AD转换输出的数据，输出y(n)为16位数据。将实现的二阶节在QuartusII中进行编译综合后，在波形图中分别给定不同的滤波器系数和输入不同的序列时，进行了波形仿真，这里给出其中的一个仿真波形如图2所示(图2是实现系统函数为：H(z)=(5+5z-1+5z-2)/(1-z-1-z-2) 的二阶节的波形图，其中a0、a1、a2、b0、b1为滤波器系数，xn为输入序列，yn为输出序列)。

下面将对用FPGA实现的二阶节时序波形仿真值和用Matlab对二阶节的仿真结果相比较，分别对在输入序列相同、但滤波器系数不同和滤波器系数相同、但输入序列不同等几种情况分别进行了比较，比较结果如表1所示。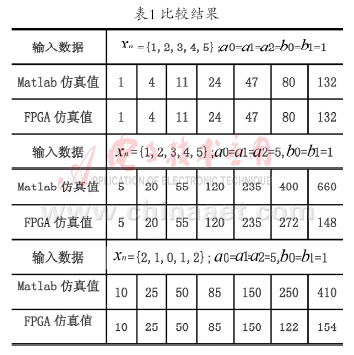

由表1可以看出所设计的二阶节在不同系数和不同输入情况下的FPGA仿真值和由Matlab计算值基本一致，说明采用