快速傅里叶变换与多项式乘法有什么关系

速度。在此过程中，我们的 工作最关键的就在于以O（n*logn）的时间快速把一个多项式从系数形式转换为点值形式（求值，我们即称之为FFT），然后再以O（n*logn）的时 间从点值形式转换为系数形式（插值，我们即称之为FFT逆）。最终达到了我们以最终的系数形式表示的多项式的快速乘法为O（N*logN）的时间复杂度。 好不令人心生快意。

    对上图，有一点必须说明，项w2n是2n次单位复根。且不容忽视的是，在上述两种表示法即系数表示法和点值表示法相互转换的过程中， 都使用了单位复根，才得以在O（n*logn）的时间内完成求值与插值运算（至于何谓单位复根，请参考相关资料。因为为了保证本文的通俗易懂性，无意引出 一大堆公式或定理）。

第三节、FFT

     注：本节有相当部分文字来自算法导论中文版第二版以及维基百科。

     在具体介绍FFT之前，我们得熟悉知道折半定理是怎么一回事儿：如果n>0且n为偶数，那么，n个n次单位复根的平方等于n/2个n/2个单 位复根。我们已经知道，通过使用一种称为快速傅里叶变换（FFT）的方法，可以在O（n*logn）的时间内计算出DFTn（a），而若采用直接的方法复 杂度为O（n^2）。FFT就是利用了单位复根的特殊性质。

    你将看到，FFT方法运用的策略为分治策略，所谓分治，即分而治之。两个多项式A（x）与B（x）相乘的过程中，FFT用A（x）中偶数下标的系数与奇数下标的系数，分别定义了两个新的次数界为n/2的多项式A[0]（x）和A[1]（x）：

A[0](x) =a0 +a2x +a4x2 +··· +an-2xn/2-1,
A[1](x) =a1 +a3x +a5x2 +··· +an-1xn/2-1.

    注意，A[0]包含了A中所有偶数下标的系数（下标的相应二进制数的最后一位为0），而A[1]包含A中所有奇数下标的系数（下标的相应二进制数的最后一位为1）。有下式：

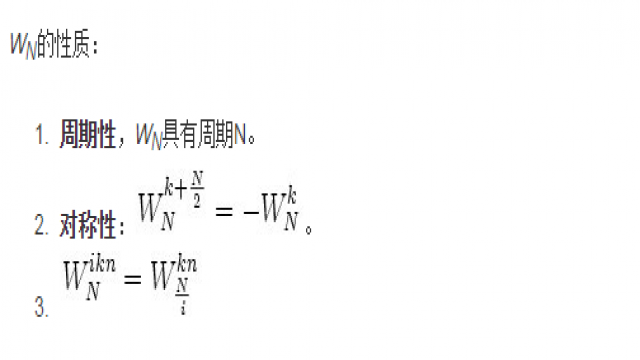
    为了简单起见，我们下面设待变换序列长度n = 2r。 根据上面单位根的对称性，求级数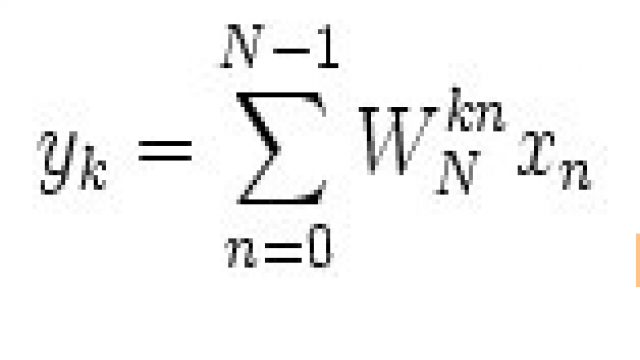

时，可以将求和区间分为两部分：

奇数号和偶数号序列N/2点变换。由此式只能计算出yk的前N/2个点，对于后N/2个点，注意Fodd(k) 和 Feven(k) 都是周期为N/2的函数，由单位根的对称性，于是有以下变换公式：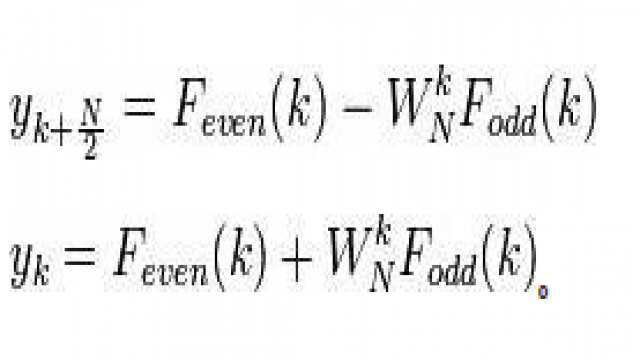

    这样，一个N点变换就分解成了两个N/2点变换，照这样可继续分解下去。这就是库利-图基快速傅里叶变换算法的基本原理。此时，我们已经不难分析出此时算法的时间复杂度将为O(NlogN)。

     ok，没想到，本文之中还是出现了这么多的公式（没办法，搞这个FFT就是个纯数学活儿。之前买的一本小波与傅里叶分析基础也是如此，就是一本数学公式和定理的聚集书。不过，能看懂更好，实在无法弄懂也只权当做个稍稍了解）。

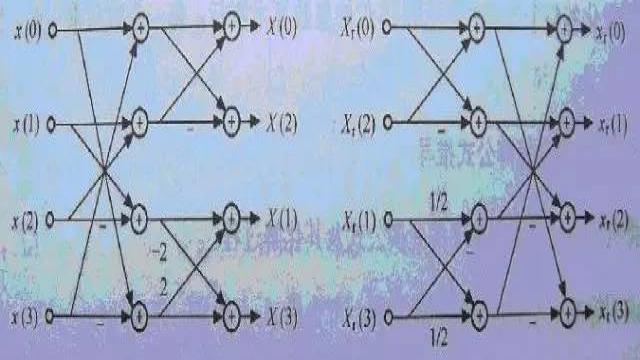
    好了，下面，咱们来简单理解下FFT中的蝶形算法，本文将告结束。如下图所示：

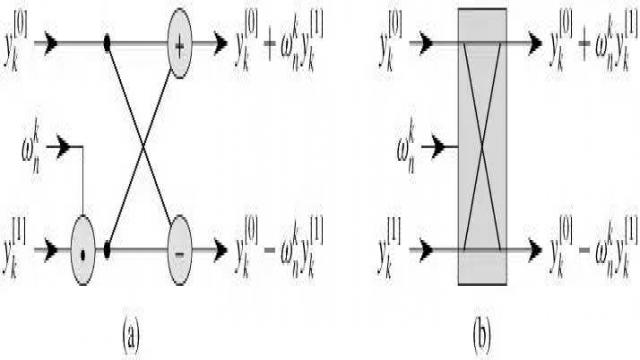      有人这样解释蝶形算法：对于N（2的x次方）点的离散信号，把它按索引位置分成两个序列，分别为0，2，4，....，2K（记为A）和 1，3，5，....，2K-1（记为B），由傅立叶变换可以推出N点的傅立叶变换前半部分的结果为A+B*旋转因子，后半部分的结果为A-B*旋转因 子。于是求N点的傅立叶变换就变成分别求两个N/2点序列的傅立叶变换，对每一个N/2点的序列，递归前面的步骤，直到只有两点的序列，就只变成简单的加 减关系了。把这些点的加减关系用线连接，看上去就是个蝶形。ok，更多可参考算法导论第30章。

      举一个例子，我们知道，4X4的矩阵运算如果按常规算法的话仍要进行64次乘法运算和48次加法，这将耗费较多的时间，于是在H.264中，有一种改进 的算法（蝶形算法）可以减少运算的次数。这种矩阵运算算法构造非常巧妙，利用构造的矩阵的整数性质和对称性，可完全将乘法运算转化为加法运算。如下图所 示：