理解串行数据测试中的总体抖动算法

在高速串行数据的测试中，抖动的测试非常重要。在串行数据的抖动测试中，抖动定义为信号的边沿与其参考时钟之间的偏差。对于抖动测量值的量化，通常有抖动的峰峰值和有效值这两个参数。不过，抖动的峰峰值随着测量时间的增加，测量值不断变大，不能将抖动值与误码率直接联系起来，所以对于抖动测试，抖动的峰峰值并不是一个理想的指标来很衡量器件和系统的性能。
总体抖动（Total Jitter，简称Tj）为某误码率（Bit Error Ratio，简称BER）下抖动的峰峰值，在很多串行数据的规范中通常需要测量误码率为10e-12的Tj，简写为Tj@BER=10e-12。对于BER小于10e-8的Tj的测量，通常只有误码率测试仪BERT可以直接测量到。对于示波器，假设该高速信号为2.5Gbps的PCIe，单个bit的时长为Unit interval = 400ps，假设示波器采样率为20G采样率，则1个bit上包括了400ps/50ps = 8个采样点，一次分析1M个bit需要8M的存储深度，如果要测量10个比特的抖动，需要让示波器在8M的存储深度下扫描100次，由于示波器在8Mpts时计算抖动已经很耗时，重复100次的测试时间会非常长。所以示波器测量小于10e-12的误码率时的总体抖动必须通过某些算法来估算Tj。

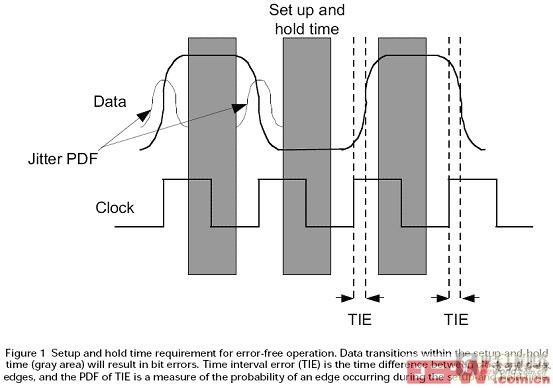
图1：TIE抖动图示与抖动概率密度函数（PDF）

基于示波器求解抖动的算法通常在三个领域观察和分析，即时域、频域、统计域。比如TIE track即为TIE抖动在时域的函数；在频域分析抖动的频谱，可以计算周期性抖动Pj和随机抖动Rj；TIE直方图、Tj的概率密度函数（Probability Density Function，简称PDF）是在统计域来分析抖动。
对于总体抖动的计算，通常从统计域分析，即分析抖动的直方图、概率密度函数PDF和累计分布函数（Cumulative Distribution Function，简称CDF）。
概率密度函数PDF的定义为：对于实数随机变量X，任何满足下列条件的函数
都可以被定义为其概率密度函数 :
在下图2中简要描述了从TIE直方图生成PDF、CDF、浴盆曲线Bathtub curve的过程。
在第一步的图示中，X轴是抖动的值，Y轴是某个抖动值上的样本数量，示波器测量每个信号每个边沿与参考时钟的偏差（即TIE），统计在某个抖动值上边沿的数量，得到TIE的直方图；
第二步中对直方图做归一化，即直方图中每个方柱子的数量除以样本总数，得到每个抖动值的发生概率，在这一步中即可得到TIE的概率密度函数PDF；

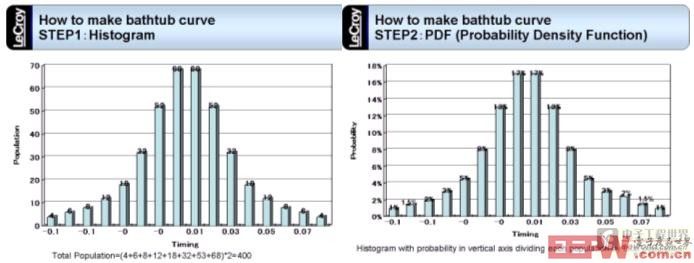
图2：抖动的直方图与PDF
在第三步中，对PDF的直方图从左右两边向中央进行积分。假定信号边沿相对理想位置超出距离x时，可能导致误码，误码率是对PDF从x到∞或-∞的积分（当x大于0时为∞，小于0时为-∞）：BER(x) =
=1-CDF(x)。然后，对Y轴取对数后如下图3中深蓝色直方图。所示，由于测试样本较少，最矮的直方图的概率（即误码率）仅1%=10e-2，要计算10e-12的BER，需要对现有的BER直方图进行外插值；
在第四步中（如下图3中Step4的图片）显示了外插值后的BER图，绿色的柱子是外插值得到的，在图上测量10e-12时抛物线形状的BER曲线的内侧的宽度，即可得到Tj；
第五步中把外插值后的BER图（类似于抛物线的曲线）以x=0分割成两条曲线后，设定横轴的最大值为0.5UI（Unit interval，即一个比特的宽度），最小值为-0.5UI，即水平方向正好一个UI的宽度，把Step4中生成的BER图左半部分的曲线右移靠最右边，右半部分的曲线左移靠最左边，即可得到浴盆曲线Bathtub curve。

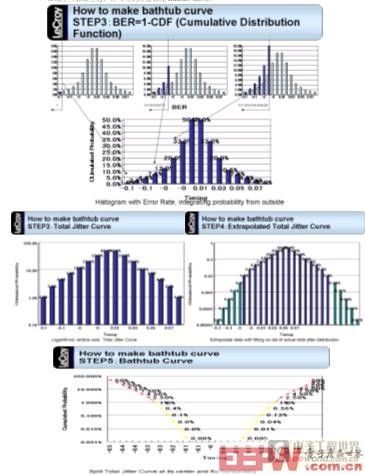
图3：抖动的PDF/BER/CDF与浴盆曲线

当然，在上述的Tj求解过程中，除了BER图中的外插值部分，其他都是基于实测结果计算的，所以BER图的外插值是示波器的抖动分析算法中最关键的一部分。外插值算法的模型精准度决定了Tj计算的精度。由于外插值算法是对实测的BER/CDF图中尾部进行拟合和外插值，在国外的相关文献中称为tail-fit算法。
在业界除了对BER图进行外插值以获取小误码率的Tj这种方法外，另外一种方法是对PDF进行外插值，得到BER10e-12的PDF，然后积分得到BER/CDF和浴盆曲线，从而算出Tj。两种算法分别称为PDF尾部拟合算法（tail-fit method for PDF）和BER/CDF尾部拟合算法（tail-fit method for the BER/CDF）。
下面简要介绍一种tail-fit method for PDF方法。如下图4所示:
第一步统计TIE分布的直方图，测量的样本数量越多，推算的Tj越准确，在下面的TIE直方图中包括了102.6k个样本；
第二步对TIE直方图的Y轴（即样本数量）取对数，把Y坐标变为对数坐标，对数运算后直方图的轮廓近似为二次方程曲线；
第三步使用最小二乘法对两个尾部进行拟合；
第四步对直方图的尾部进行外插值，归一化后可得到BER=10e-16 的概率密度函数；
第五步对每一个偏移值x进行积分：BER(x) =
=1-CDF，得到BER/CDF曲线；
第六步测量某误码率下CDF曲线的宽度即为总体抖动Tj。