CCD测量系统中基于自适应相关算法的动态目标跟踪

摘要：相关匹配是目标跟踪和模式识别的一种重要方法。介绍了CCD（电荷耦合器件）误差测量系统光学原理；针对该测量系统实际情况，提出了用相关算法实现目标位置的测量；使用自适应相关匹配的方法，实现了对连续视频图像中动态目标的跟踪；给出了实验结果，并对算法提出了改进的意见。

基于相关算法的目标跟踪是利用从以前图像中获得的参考模板，在当前图像中寻找最相似的区域来估计当前目标位置的方法。它对于背景复杂、会有杂波噪声的情况具有良好的效果。CCD（电荷耦合器件）测量技术是近年来发展迅速的一种非接触式测量技术。CCD摄像器件在分辨率、动态范围、灵敏度、实时传输方面的优越性是其它器件无法比拟的，在动态飞行目标跟踪测量中发挥着重要的作用。作者在CCD测量系统中使用相关匹配的方法，实现了对连续视频图像中动态目标的跟踪。

1 CCD误差测量系统原理

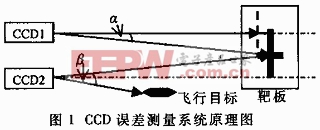
在同一观测位置布置两台CCD，其视轴平行。其中CCD1用于瞄准，CCD2用于跟踪飞行目标。CCD1瞄准线和视轴重合，获得瞄准线和靶标之间的偏差角α。CCD2获得飞行目标和靶标之间的偏差角β。系统要求得到瞄准线和飞行目标之间的水平和垂直方向上的偏差角ψx、ψy。因此规定CCD的视场中均以靶标十字中心为原点，向左和向上为正方向，将α、β分别投影到坐标轴上得到水平和垂直方向上的偏差角αx、αy、βx、βy。两台CCD的视频轴平行，视轴间距远远小于CCD到目标的距离，因此可以认为两CCD的视轴重合。所以有：

ψx=αx-βx，ψy=αy-βy (1)

图1是系统的原理图，图中靶板上的黑十字是靶标，虚线十字为瞄准分划板在靶板上的投影（由于实际靶板上没有，所以用虚线表示）。

2 图像处理算法的选择

从系统的原理分析可知，要完成偏差角度的测量首先应当从图像中提取出各个目标在图像中的位置，再根据CCD当量（每像元对应的弧度数）算出水平和垂直方向的偏差角。从CCD1的图像中的最靶标十字和瞄准分划板的位置，从CCD2的图像中提取靶标十字和飞行目标的位置。

由于飞行目标几乎贴地飞行，CCD视场中有复杂的地面背景。而且靶标是不发光的暗目标，与背景灰度反差不大，很难将目标从背景中分离出来，因此只有采用相关处理技术来进行目标识别，才能实现瞄准误差和飞行轨迹的测量。相关算法非常适合在复杂背景下识别和跟踪运行目标。由于系统图像处理是事后处理，处理连续的大量视频图像，实时性要求不高，而对处理精度和自动处理程度要求较高，因此采用该算法。

本系统中相关处理将预先选定的目标或目标特定位置作为匹配样板，求取模板和输入图像间的相关函数，找出相关函数的峰值及所在位置，求判断输入图像是否包括目标图像及目标位置。

3 相关算法的原理及改进

在机器识别事务的过程中，常把不同传感器或同一传感器在不同时间、成像条件下对同一景物获取的两幅或多幅图像在空间上对准，或根据已知模式在另一幅图像中寻找相应的模式，这就叫做匹配。如果被搜索图中有待寻的目标，且同模板有一样的尺寸和方向，在图像匹配中使用相关匹配，就是通过相关函数找到它及其在被搜索图中的位置。

3.1 相关算法

基于相关的目标跟踪寻找最佳匹配点，需要一个从以前图像中得以的模板。在图2中设模板T为一个M×M的参考图像，搜索图S为一个N×N图像（MN），T在S上平移，模板下覆盖的那块搜索图叫做子图Si,j，（i,j）为子图左上角点在S中的坐标，叫参考点。比较T和Si,j的内容。若两者一致，则它们的差为0。用误差的平方和作为它们相似程度的测度：

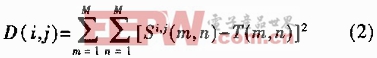
展开公式（2），则有：

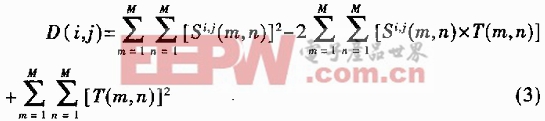
公式（3）右边的第三项表示模板的总能量，是一个常数。第一项是模板覆盖下的子图能量，随（i,j）位置而缓慢改变。第二项是子图和模板的互相关，随（i,j）改变。当模板和子图匹配时刻值最大。因此可以用以下相关函数做相似性测度：

根据柯西-施瓦兹不等式可知公式（4）中0R（i,j）≤1，并且仅在Si,j(i,j)/[T(m,n)]为常数时，R(i,j)取最大值（等于1）。相关法求匹配计算量很大，如图2所示的情况，要在（N-M+1）×（N-M+1）个参考位置上做相关计算，每次相关计算要做3M2次加法、3M2次乘法、1次除法、2次开方运算。由于乘除法运算量最大，整个算法的时间复杂度大约为o((N-M+1) ×2×(3M2+1))。整个运算过程中，除了匹配点一点以外，都是在非匹配点上做无用功。但是，模板匹配算法准确度较高，适合对大量的连续视频图像做自动处理。

3.2 自适应的相关匹配

在相关匹配过程中目标的