高阶电路动态特性的仿真分析

作者/ 贺为婷 杨建华 西安工业大学 电子信息工程学院(陕西 西安 710032)

摘要：为了准确直观地观测电路的动态变化过程，采用四种方法对一电路实例进行仿真分析：用积分法求解状态方程，用拉普拉斯变换法求解s域的方程组，用数值积分函数求微分方程的数值解，构建微分方程的Simulink模型观测响应曲线。四种方法的仿真结果完全一致且与电路理论相符。实验结果表明，Matlab程序简洁、可读性强且计算结果准确，同时它形象直观，改变参数方便，能够弥补硬件实验的不足。Matlab在电路理论学科研究与工程实践中都具有很好的应用价值。

引言

高阶动态电路的分析通常都归结为高阶微分方程或一阶微分方程组的求解，需要微分方程和矩阵理论的相关知识，掌握起来比较困难。对于复杂的高阶电路，用求解微分方程的方法则更加困难，一是列写微分方程，二是根据变量及变量的各阶导数的初始值确定积分常数。若借助合适的仿真软件，则可以使电路的分析变得方便、准确和直观。电路仿真是电路分析及电路教学的重要手段，它形象直观，改变参数方便，能够弥补硬件实验的不足^[1]。

Matlab是目前最为流行的工程软件之一，它具备强大的计算、仿真和绘图功能，能方便地绘制二维、三维图形和相量图。运用该软件，可以方便地研究各类系统问题，包括电路仿真分析。对于动态过程，用图形来显示会更加直观，它可动态地演示复杂电路各参量的变化过程，从而加深对电路的理解和认识。对于动态过程中某时刻的情况可以有一个定量的认识，对工程上解决系统处在动态阶段的问题有一定的指导意义[2]。

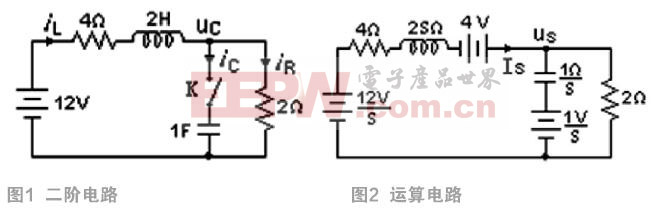
本文以求解图1所示电路的电容电压和电感电流为例，介绍四种基于Matlab的电路动态过程的分析方法。

1 积分法求解状态方程

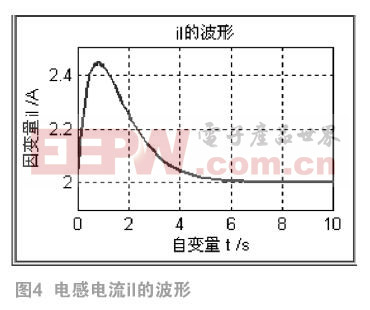
一个二阶电路如图1所示，开关K原来是打开的，电路已经稳定，uc(0)=1V，il(0)=2A。电源电压及各元件的参数值标示于图中。在t=0时，将开关K闭合，求t≥0时的电容电压uc(t)及电感电流il(t)的变换规律^[3]。

积分法求解状态方程：如果一个系统的状态描述方程为：

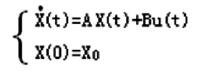
则该系统的状态响应为：

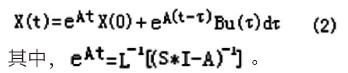
其中。

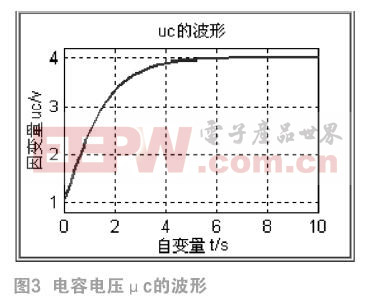
对于图1所示的电路，以电容电压uc和电感电流il为状态变量，则建立电路的状态方程为：

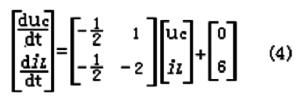
编程求解状态响应uc(t)与il(t)：

syms x1 x2 s t z ;

A=[-1/2,1;-1/2,-2]; Bu=[0;6];

X=[x1;x2];X0=[1;2];

Asi=eye(2)*s-A; % s*I-A;

AA=inv(Asi); % [s*I-A]-1;

eAt=ilaplace(AA); %e A t=L-1[([sI-A]-1];

eAtz=subs(eAt,t,t-z); %求eA(t-z);

X= eAt*X0+int(eAtz*Bu,z,0,t); % Bu= B*u(z);

uc=X(1), il=X(2)

运行程序得：

uc = 3*exp(-3/2*t)-6*exp(-t)+4

il = -3*exp(-3/2*t)+3*exp(-t)+2

即电容端电压和电感中电流的解析解为：

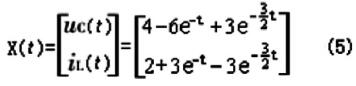
积分法求解电路响应的过程是：以电容电压和电感电流为状态变量建立电路的状态方程;根据状态方程确定矩阵A、B;求矩阵指数eAt;根据方程式(2)求状态变量的解析表达式，最后求出要求电量的解析表达式^[4]。

2 用Matlab拉普拉斯变换法求解

时域分析法用于高阶电路的分析计算时，确定初始条件和积分常数非常繁琐。可采用拉普拉斯变换法来求解。将时域电路变换为复频域电路，即运算电路[5]。在运算电路的基础上，用与直流电阻电路相同的方法进行分析，建立s域描述方程。通过对s域方程的运算，得到电路中待求电量的象函数F(s)，对象函数F(s)进行拉氏反变换就得到对应的时域解f(t)。

图1对应的运算电路如图2所示，由运算电路得：

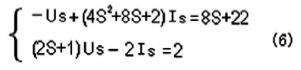
针对方程组(6)进行MATLAB编程：

syms t s;

A=[-1 4*s^2+8*s+2;2*s+1 -2];

B=[8*s+22;2];

AA=inv(A); %A的逆阵;

X=AA*B;

Us=X(1); %电容电压的象函数;

Is=X(2); %电感电流的象函数;

Uc(t)=ilaplace(Us), il(t)=ilaplace(Is)

程序运行结果为：

Uc(t) =3*exp(-3/2*t)-6*exp(-t)+4

Il(t) =-3*exp(-3/2*t)+3*exp(-t)+2

该结果与方法1的结果完全一致，即电容电压uc(t)和电感电流il(t)的解析表达式同式(5)。

3 用ODE函数求微分方程的数值解

基于龙格-库塔法，MATLAB提供了一套求常微分方程数值解的函数，可以根据不同的对象选择不同的算法。其函数格式如下：

[X,Y]=ode23(‘f’,[x0,xn],Y0)

[X,Y]=ode45(‘f’,[x0,xn],Y0)

其中：X，Y是两个相量，X对应自变量x在求解区间[x₀, x_n]的一组采样点，其采样密度是自适应的，无需指定;Y是与X对应的一组解。f是一个M函数文件，代表待求解方程。[x0,xn]代表自变量的求解区间。Y0=Y(X0)，由方程的初值给定。函数在求解区间[x₀,x_n]内，自动设立采样点向量X，并求出解函数Y在采样点X处的样本值^[6]。

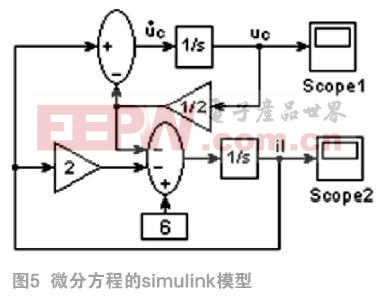
本文选用采用了四阶、五阶龙格-库塔法的ode45函数，它采用自适应变步长的求解方法