高阶电路动态特性的仿真分析

，即当解的变化较慢时，采用较大的步长，从而提高了计算速度;当解的变化较快时，步长会自动地变小，可以提高计算的精确度。

图1的状态方程为式(1)，初始条件为：uc(0)=1V，il(0)=2A，MATLAB程序如下：

function dy = myfun (t, y); % 将方程式定义为函数文件并取名存盘以便调用

dy= zeros(2,1); %变量y为两行一列相量

dy(1)= -1/2*y(1)+ y(2);

dy(2)= -1/2*y(1)-2*y(2)+6;

[t,y]= ode45(‘myfun’,[0,10],[1,2]); % 调用ODE函数并代入初始条件

t’; %转置显示自变量的一组采样点

y(:,1)’;y(:,2)’;% 转置显示y(1)、y(2)与采样点对应的一组数值解

uc= y(:,1);

il = y(:,2);

plot(t,uc,’linewidth’,1.5);%绘制uc波形，波形线宽为1.5

grid; set(gcf,’color’,’w’) % 打开网格;使输出图形的背景为白色

axis([0 10 0.8 4.2]); % 设定坐标轴的范围

set(gca,'xtick',[0 2 4 6 8 10]); %设置x轴刻度标示

set(gca,'ytick',[1 2 3 4]); %设置y轴刻度标示

xlabel(‘自变量t /s’) ; % x轴加注释

ylabel(‘因变量uc /v’); % y轴加注释

title(‘uc的波形’); % 图形正上方加注释

figure; %打开第二个图形界面

plot(t,il,’linewidth’,1.5); %绘制il波形，波形线宽为1.5

grid; set(gcf, ‘color’, ’w’);

axis([0 10 1.9 2.5]); %设定坐标轴的范围

set(gca,'xtick',[0 2 4 6 8 10]);

set(gca,'ytick',[2 2.2 2.4]);

xlabel(‘自变量t /s’);

ylabel(‘因变量il /A’);

title(‘il的波形’);

在此，由于篇幅有限，没有显示自变量的采样点和与采样点对应的数值解，而只是将解以图形的方式输出，如图3和图4。从结果看出，用数值积分ODE函数求解状态方程简单方便，易于理解和掌握。与其它语言程序相比，可大大节省编程时间[7]。

4 构建微分方程的simulink模型求解

对于形如y''=ay'+by+c的微分方程，构建simulink模型的核心思想是：y''经过积分得y'，y'经过积分得y，而y'、y经过代数运算又可得到y''。由微分方程式(4)得：

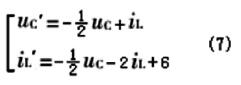
根据式(7)，可构建出图5所示的simulink模型。其中用到两个积分模块、两个求和模块、两个比例模块和一个恒定模块。两个示波器用于输出uc和il的图形^[8]。

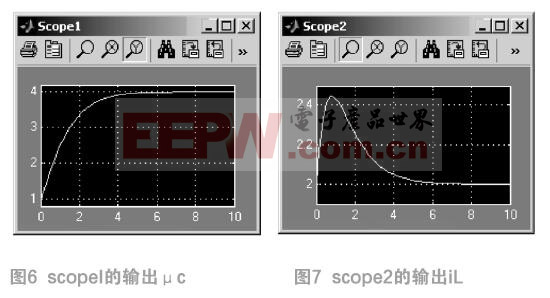
simulink模型建成以后，要对uc和il设置初值：uc(0)=1V，il(0)=2A，双击uc模块将初始值设为1V，双击il模块将初始值设为2A。设置示波器的信号显示范围：scope1,t:0—10s,Y:0.8—4.2;scope2,t:0—10s,Y:1.9—2.5。

开始仿真：选择simulation下的parameter命令，设置仿真的start time为0s，stop time为10s。最后选择simulation下的start命令进行仿真，或击模型窗口工具栏上黑色右三角图标进行仿真。

双击示波器scope1和scope2，则会得到图6和图7，与图3和图4的uc和il曲线完全相同，即两种仿真结果一致。

5 结论

通过本文介绍的几种动态电路的分析方法看到：积分法求解动态电路，以电容电压和电感电流为状态变量建立电路的状态方程，根据状态方程求出状态变量的解析表达式;用ODE函数求解微分方程组，对求解动态电路带来了极大方便，并给出了解的直观图形;利用Matlab语言直接进行拉氏变换求解动态电路，大大提高了计算效率;而利用Matlab的Simulink功能得到了一种全新的求解暂态电路的思路。 Matlab的编程效率高、语言简练、绘图方便。运用Matlab可使电路的分析运算变得方便和快捷。运用Matlab语言编程和Simulink仿真的方法对复杂电路进行分析和计算，不仅可以节约计算时间、方便地调试电路参数，还可以通过图形非常直观地观察到其响应的过渡过程[10]。所以Matlab在电路理论学科研究与工程实践中都具有很好的应用价值。

参考文献：

[1] 张洪宝.Matlab在动态电路分析中的应用[J]. 鲁东大学学报, 2009(2):144—147.

[2] 王光亮.用Matlab编程实现动态电路仿真[J].江西电力职业技术学院学报,2007(3):8-10.

[3]杨红权,辜承林.Matlab符号运算在电路分析中的应用[J].电气电子教学学报,2008(1):23-26.

[4]蔡启仲.控制系统计算机辅助设计[M].重庆:重庆大学出版社,2003.8.

[5]邱关源.电路[M].北京:高等教育出版社,1999.

[6]于润伟.Matlab基础及应用[M].北京:机械工业出版社,2003.10.

[7]张颖,甘正佳,金维香.基于Matlab的暂态电路分析与计算[J]. 长沙电力学院学报,2002(3):44-47.

[8]王群, 耿云玲. Simulink在电路分析中应用[J].电力自动化设备, 2007(4):71-75.

[9]陈怀琛.M at lab及在电子信息课程中的应用[M].北京:电子工业出版社,2002.

[10]黄忠霖,黄京.Matlab符号运算及其应用[M].北京:国防工业