H桥Buck变换电路输出电压幅相特性的研究
1引言
单相H桥可逆变换电路作为软开关逆变器和功率变换电源研究的核心技术之一,在电力传动、电力系统无功与谐波补偿和可再生能源发电等领域应用广泛。作为单相H桥电压型变换拓扑主体的Buck变换电路结构,因在宽输入电压范围和宽负载范围等方面具有杰出的性能表现,而被广泛应用。基于Buck变换机理的功率变换电路,输出电压的交流成分特性是其最重要的性能指标之一。在输入电压确定的条件下,有关输出电压交流成分的幅值与滤波电容、电感、工作频率、输出电压之间的关系,在不少文献[3]中已经给以理论和定量分析,但在不同占空比下,输出电压交流成分与电流之间存在不同的移相关系问题,几乎无人问津。其实这种移相关系,是对变换器输出特性、滤波器幅相特性以及与负载之间的能量交换特性的集中反映,对于深入研究单相H桥电压型变换器的输出特性和滤波器设计,具有重要的学术理论价值和实际意义。本文从单相H桥Buck变换器的工作原理出发,对其输出电压特性进行研究,同时从数学理论分析的角度,结合电容充电的物理过程,研究其交流电压成分与电流之间的移相角大小受占空比变化影响的定量关系,并进行定性分析,利用MATLAB/SIMULINK建立了其仿真模型,仿真研究结果验证了理论推导和分析的正确性。
2单相H桥Buck变换电路的工作原理
单相桥式Buck电路如图1所示,采用IGBT作为开关器件,负载为阻感性负载。为保证电路的四象限运行,每个IGBT反并联一个二极管作逆导开关;为滤除输出电压中对应开关频率及其谐波成分的交流分量,变换电路中加入LC低通滤波器,其截至频率远小于开关频率。设IGBT的周期为TS,触发导通信号的占空比为D,变换电路中IGBT按PWM变化规律控制:在一个周期的一定时间内(0≤t≤DTs),同时给IGBT1及IGBT4导通信号,使电感电流iL增大(正方向如图1所示);在互补时间内(DTs≤t≤Ts),关断IGBT1及IGBT4,同时给IGBT2和IGBT3导通信号。当IGBT1及IGBT4导通时,电源电压Vg对电容充电,负载输出电压增大;当IGBT2及IGBT3导通时,电容放电,输出电压减小。在IGBT1及IGBT4关断时,二极管D2和D3为正向电感电流提供续流通路,实现无功能量的回馈;当IGBT2及IGBT3关断时,二极管D1和D4为反向电感电流提供续流通路,从而保证变换电路的四象限运行。
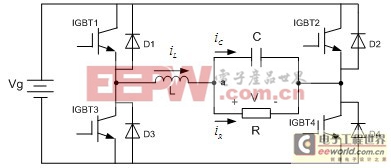
图1单相桥式Buck电路图
改变一个周期内IGBT1及IGBT4导通的时间,即触发信号的占空比D,可获得期望的输出电压。占空比D还可以按照正弦规律进行控制,实现SPWM逆变输出。
3单相H桥式Buck变换电路的输出电压特性
文献[2]中推导出了单相桥式Buck变换电路在稳态下的电压转换比,本文将侧重阐述Buck变换电路输出电压交流成分的特性。
在电路处于稳态下,忽略负载电压的波动,假设其为恒值V;对电源、电感L及电阻R回路列基尔霍夫电压(KVL)方程,可得电感两端电压波形如图2所示,其中T为开关周期。
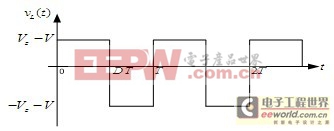
图2Buck电路电感电压波形图
根据上图,结合电感电压与电流关系式: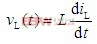 ,作电感电流iL(t)的波形如图3所示,其中I为电感电流的平均值,其值等于负载电流。
,作电感电流iL(t)的波形如图3所示,其中I为电感电流的平均值,其值等于负载电流。

图3Buck电路电感电流波形图
结合上图及图2所示的电感电压波形,可得一个周期内电感电流iL(t)表达式:
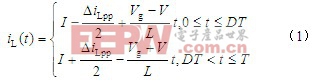
上式中,△iLpp为电感电流交流分量的峰-峰值,且满足:
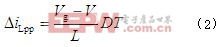
对图1中的节点a列基尔霍夫电流(KCL)方程,

对电感电流iL进行傅里叶分解,将其分解为直流分量I和呈三角波变化的纹波分量i~L,由电容器对电流的隔直通交特性,可知直流分量I将全部流过电阻R,交流分量i~L近似全流过电容器。即电容器电流iC满足:

设电容电压的交流成分为u~C,由电容电流电压关系式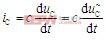 ,同时结合式(4)作电容电压交流成分及其电流波形如图4所示。
,同时结合式(4)作电容电压交流成分及其电流波形如图4所示。
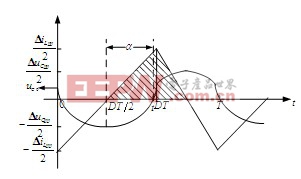
图4Buck电路电容电压交流成分及其电流波形图
由电容充电关系式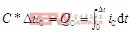 出发,对图3所示的阴影部分积分求面积有:
出发,对图3所示的阴影部分积分求面积有:
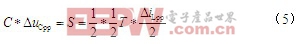
其中,△uCpp为电容电压交流成分的峰-峰值,将式(2)代入得

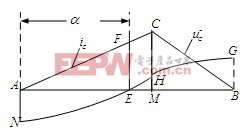
为便于从物理角度分析电容电压交流成分较电流的移相幅度及移相角的分析,对图4所示的阴影部分进行具体分析。取阴影部分如图5所示。
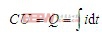 ,故有
,故有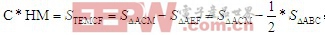 ,
,图5电
从而得到如下关系式
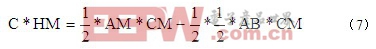
结合图4,代入线段AM、AB、CM及HM值,解得
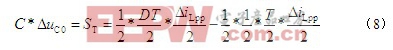
将式(2)、式(6)代入式(7),解得
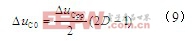
又由于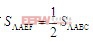 ;得如下关系式
;得如下关系式
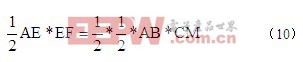
将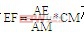 及AM=D*AB代入上式得
及AM=D*AB代入上式得
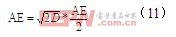
AE对应α角度,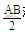 对应90°,故得
对应90°,故得

以上是从电容充电的物理关系角度,推导电容电压交流成分较其电流的相移问题。下面从数学积分的角度作推导。
由图4可知,电容电流在DT/2及(1+D)T/2时刻为零。而电容电流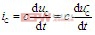 ,可知电容器电压交流成分u~C在T+DT/2及(2+1+D)T/2时刻分别取最小值及最大值。设u~C的峰-峰值为△uCpp,则稳态下,有:
,可知电容器电压交流成分u~C在T+DT/2及(2+1+D)T/2时刻分别取最小值及最大值。设u~C的峰-峰值为△uCpp,则稳态下,有:
- 一种逆变H桥IGBT单管驱动以及工作保护方案(11-29)
- 一种掉电自动开阀的采暖室温控制器电路设计(11-27)
- 基于PWM技术的直流电机控制系统(08-23)
- 基于BD6225芯片的H桥电机驱动器(05-23)
- 详细解析Buck电路开关电源纹波的有效抑制方法(01-23)
- 基于Buck电路的开关电源纹波的计算和抑制(05-27)
