高频和微波功率基准及其应用研究----微量热计基本理论研究(二)
=P1RF +P1DC(t),则有 将式(2-27)代入式(2-28),可得 其中P2RF和P1RF分别是热敏电阻和功率座壁上吸收的高频和微波功率,即式(2-25)中的PTRF和Ploss。 由于热敏电阻平衡电桥和反馈控温环路的作用,T2始终不变,T1也始终不变,令第一阶段电桥平衡后的辅助加热功率与第二阶段的辅助功率之差为ΔP1DC,化简式(2-29)有则 有效效率为 即有效效率始终与效率相等。 2.4.2.2升温方式 升温方式微量热计的结构如图2-11所示。 所谓升温是指在这种设计中,没有反馈控温环路,加入高频和微波功率会导致T1的变化,由于T1稳态温升与P2DC及Ploss的比例系数可以求得,就可以根据加入高频和微波功率后的稳态温升计算Ploss。 在直流偏置阶段,没有输入任何功率时,热敏电阻、功率座壁和等温绝热壁的初始温度相等,为T0;当加入功率时,只由热敏电阻平衡电桥提供直流功率,P1 =0;达到初始平衡后,P2 =P 2DC1,则有 由此得到功率座壁在本阶段的稳态温升为 在高频和微波功率替代阶段,加入高频和微波功率后,P2 =P2RF+P2DC(t),P1 =P1RF,由式(2-26)得 式(2-32)和式(2-34)联立,可解得在本阶段功率座壁温升的表达式 及 则有效效率为 有效效率与效率之差为 达到稳态后,有效效率为 有效效率与效率之差变为 根据式(2-40)计算得到的有效效率与效率偏差曲线如图2-12所示。 其中从低到高依次是效率ηs为0.95、0.9、0.8时有效效率与效率的偏差随G21/G10变化的曲线,由图2-12可见采用升温方法测量的有效效率总是大于效率,对ηs较小的功率座,两者差异较大;对同一个功率座,ηs和G21固定,G10是影响二者差异的原因。 式(2-37)是升温方式有效效率的理论表达式,但不能用于有效效率的测量,因为在测量时能够获得的测量数据只有ΔP2DC(t)和ΔT1(t),无法使用式(2-37)计算有效效率,还是需要达到稳态才能计算出稳态时的有效效率。 达到稳态后,功率座壁在本阶段的稳态温升可由式(2-35)可求得。 式(2-34)变为 即得 则有效效率的稳态表达式式(2-39)也可以写为 根据式(2-44)就可以使用实际测量结果计算有效效率的稳态值 ![]()
![]()
![]()
![]()

![]()
![]()

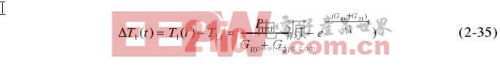
![]()


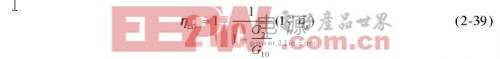


![]()

![]()

- 电源设计小贴士 1:为您的电源选择正确的工作频率(12-25)
- 用于电压或电流调节的新调节器架构(07-19)
- 超低静态电流电源管理IC延长便携应用工作时间(04-14)
- 电源设计小贴士 2:驾驭噪声电源(01-01)
- 负载点降压稳压器及其稳定性检查方法(07-19)
- 电源设计小贴士 3:阻尼输入滤波器(第一部分)(01-16)
