基于FPGA的数字下变频的研究与实现

0 引 言
受现有技术水平的制约，在目前的信号变频体制中大部分是首先将射频信号通过一次或者几次的模拟下变频转换到中频上，在中频对信号数字化，然后再进行数字下变频。数字下变频是软件无线电的核心技术之一。随着WiMAX等宽带无线通信技术的逐渐成熟，对无线设备数字带宽的要求也越来越高，所以，有必要对带宽较宽信号的数字下变频进行研究。

l 常用数字下变频结构
通常的数字下变频结构如图1所示。可以把数字下变频分为两个基本的模块，数控振荡器：NCO(Nu-merical Control Oscillator)混频模块和抽取滤波模块。其中NCO模块产生正余弦波样本值，然后分别与输入数据相乘，完成混频。
抽取滤波模块常用的结构是积分梳状抽取滤波器(CIC)级联后再与多级半带滤波器(HBF)的级联。如果信号带宽比较宽，抽取倍数不是很大，可以采用FIR滤波器。当输入信号采样速率很大的时候，则可以采用多相滤波的下变频方案，把运算环节安排在抽取之后，这种结构大大降低了对数据处理速度的要求。

2 信号下变频方案的设计
设信号的中频频率为典型值70 MHz，带宽为lO MHz，则基带带宽B为5 MHz。由Nyquist采样定理，对该信号的采样频率不能低于2B即10 MHz，实际应用中一般大于2．5B即12．5 MHz。现阶段商用数字下变频芯片都是基于CIC和HBF级联方式设计的，当采样率大抽取倍数小时，芯片处理带宽比较窄，滤波器组的滤波性能也不理想。同时DSP芯片数据处理速度达不到要求，所以采用FPGA实现该数字下变频系统。
2．1 采样频率fs的确定
由于过采样的频率要求达到150 MHz以上，速率比较高，不易实现，所以设计方案采用带通采样。由Shannon带通采样定理，设f(t)为一带通信号，其通稀为(fL，fH)，在实信号采样情况下，其采样频率fs应满足以下条件，才能从其采样信号重构恢复f(t)：

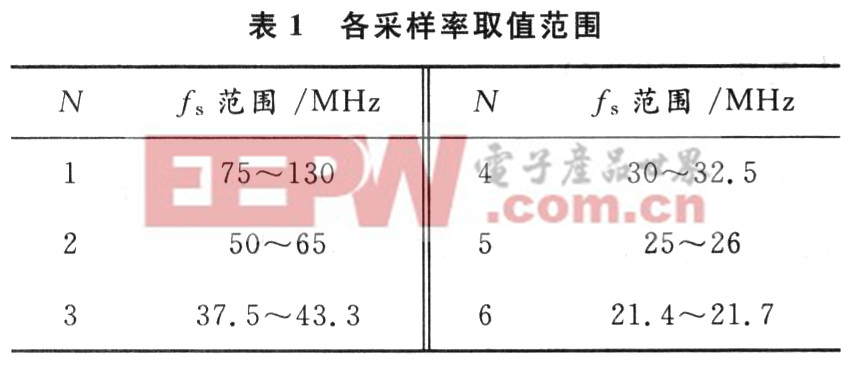
式中：N为满足后式的某一正整数。由后式可以算出1≤N≤6，当N取不同值时，各采样率取值范围如表1所示。

采样率高，ADC前的抗混叠滤波器比较容易实现，同时ADC信噪比(SNR)公式如下：
SNR=[6．02b+1．76+101g(fs／2B)]dB
式中：b是ADC的采样位数。可见采样率越高，ADC的SNR也越高。所以，应提高采样率，但是同时也应考虑到后级运算速度情况。
2．2 NCO的设计
主要的下变频方法有以下四种：
(1)查表法产生正余弦波样本值，然后混频。
(2)IIR振荡器产生数字化正余弦函数，然后混频。
(3)采用流水线技术的坐标旋转数字式计算机(CORDIC)算法。
(4)重采样。
实际中用得最多的还是(1)，(3)两种方法。
方法(1)产生以下正余弦波样本值：
s(n)=cos[2π(fc／fs)n]， n=O，1，2，…
式中：fc为NCO的本振频率，满足fc=70-fs，这些样本值与信号采样值相乘完成混频。
采用查表法要实现比较高的精度需要大量的FP-GA ROM资源，而方法(3)则不需要耗费这么大的资源，虽然采用流水线技术会使输出产生迭代次数个时钟周期的延迟，但是可以省略两个乘法器，是比较好的实现方式。
进一步研究采样率，令fs=Mfc，由s(n)的表达式知，如果M为整数时，明显样本值可以由庞大的查找表数据简化为M个数据，将fs=Mfc代入fc=70-fs中，可得：

结合表1和上式，综合考虑各种情况，取N=2，M=4，fs=56 MHz，则s(n)=cos(πn/2)，n=O，1，2，…。可以看出正余弦波样本值只为1，-1，0，混频时只是对输人数据进行保持不变，取负和置0操作，省略了两个乘法器，最大程度地节约了资源，同时也避免了正余弦值位数截断带来的非正交误差。
2．3 抽取滤波器的设计
由上面的讨论，采样率确定为56 MHz，精度为12 b。对输入数据进行四倍的抽取，所得到的数据速率为14 MHz，大于12．5 MHz，满足要求。
CIC滤波器适合窄带高抽取率的情况，用在此处并不合适，故采用FIR滤波器作为抽取抗混叠滤波器，并且把四倍抽取分为两级两倍抽取，两级抽取均使用半带滤波器。
选用System View的Linear Sys Filters进行滤波器设计，用等纹波法使设计误差在整个频带内均匀分布。第一级半带滤波器参数如下：采样率fs=56 MHz，滤波器通带截止频率为5 MHz，阻带起始频率为(56／2)-5=23 MHz，过渡带带宽为23-5=18 MHz，阻带衰减为-60 dB，通带纹波系数为0．01 dB 。由于滤波器的阻带起始频率较大，过渡带相应较宽，设计出的半带滤波器阶数只有ll阶，系数进行12 b量化后值如下：

[36，0，-230，0，1 217，2 047，1 217，0，-230，0，36]
同理，第二级半带滤波器的阶数为23阶，系数量化值为：
[-10，0，33，O，-80，0，172，0，-376，O，1 285，2 047，1 285，0，-376，0，172，0，-80，O，33，0，-10]

3 方案的FPGA实现
由以上NCO的设计可知，混频部分非常容易实现，关键部分在于滤波器的实现。
设计工具产生的半带滤波器具有对称结构，可只利用其中一半的系数。考虑到滤波器数据输入速率比较高和FPGA资源的节约，采用全并行的分布式算法(DA)滤波器，每个时钟周期能完成一次滤波运算。
以第一级滤波器为例，具体实现方式如下：
(1)由于系数的对称性，可将有相同滤波系数的输入数据先进行相加，只用其中4个系数，简化结构，节约资源。输人数据为12 b，相加后位宽扩展一位为13 b。
(2)采用全并行的DA结构，每一位数据都有一个深度为24的查找表，将数据每3位分为一组，最后一组为4位，每组查表结果移位相对应位数后相加，结果输入两级流水线加法器阵，最后得到滤波输出值。
(3)设计中应注意的三个问题：
①滤波器系数的量化，把系数扩大2L倍，最后输出右移L位即可。
②查找表的建立。由于只有4个系数，不用对系数进行分组分别查表以节省查找表资源。
③运算中数据位数的处理，不要溢出。
第二级滤波器的实现跟第一级滤波器类似。