组合BCH码在CDMA系统中的研究与应用

摘要：提出了素多项式同组的概念，并对由同组的素多项式构成的组合BCH码在码长、信息位长度、阶数等方面的特性进行了研究和分析。同时，还对组合BCH码经过群变换后产生的类正交矩阵进行了研究。研究发现，当构成组合BCH码的素多项式的个数越多时，类正交矩阵的行类正交性越好，列类正交性越差。最后，将组合BCH码的类正交矩阵用于CDMA通信系统中，并分析了在构成组合BCH码的素多项式个数不同的情况下，行和列分别作为多用户编码时的误码率。
关键词：组合BCH码；类正交矩阵；CDMA；误码率

BCH码最早是由霍昆格姆(Hocquenghem)在1959年、博斯(Bose)和查德胡里(Chandhair)在1960年各自提出的，它是一类重要的循环码，能纠正多个随机错误。本文中由BCH码或者BCH码组合得到的生成多项式，采用群变换编码方法，可以得到一种具有类正交特性的矩阵。利用矩阵的类正交特性，将其用于码分多址的多用户传输，此外，也可以将这种矩阵用于扩谱通信和通信加密等方面。

1 BCH码的组合特性
1．1 BCH码的产生
对于BCH码中的一个素多项式：

式中：xi仅表明其系数(1或0)ci的值，x本身的取值并无实际的含义。BCH码的生成多项式g(x)可以由一个素多项式构成，也可以由若干个素多项式组合而成。
BCH的码长n一般是2m-1或是2m-1的因子，通常把码长为2m-l的BCH码称为本原BCH码，而把码长为2m-1因子的BCH码称为非本原BCH码。
1．2 BCH码的组合特性
由BCH码的定义可知，对于(n，k)的生成多项式g(x)，它的阶数为m，则由g(x)产生的BCH码的码长n为2m-1或2m-1的因子。将这些生成多项式的阶数等于m，码长为n是2m-1或是2m-1的因子的素多项式放在同一组中，称为同组BCH码素多项式。对于同组的素多项式，将他们中的一个或者多个素多项式进行组合，可以得到组合BCH码，即：

由同组的素多项式构成的组合BCH码在码长、信息位长度和阶数等方面具有一些特殊的性质。组合BCH码的最高项次数为：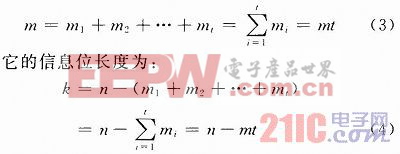


2 组合BCH码的类正交特性
2．1 互相关系数
在判断一个矩阵的正交特性的时候，往往会用到互相关系数这个概念。
在一个矩阵中，设各个码组的编码长度为n，每个码元只取+1和-1，x和y是该矩阵中的两个码组：

若码组x和y正交，则必有ρ(x，y)=0；若码组x和y不正交，则ρ(x，y)≠0，并且当码组x和y的相关性越小时，它们的相关系数ρ(x，y)越小；当码组本身与本身相乘时，有ρ(x，x)=1。
2．2 类正交矩阵的产生
在(n，k)的BCH码中，它的码长为n，信息位长度为k，BCH码的生成多项式g(x)的最高阶数为m，并且满足k=n-m。
首先，根据BCH码的生成多项式g(x)，运用群变换的编码方法，产生生成矩阵G，它是一个k×n的矩阵。

群变换后的生成矩阵G可以分为两个部分，前半部分是一个k×k阶的单位矩阵Ik，后半部分，称之为P矩阵，它是一个k×m阶的矩阵，即：

由此可以得到P矩阵的变换矩阵P’，经过研究发现，P’矩阵的行向量与行向量、列向量与列向量之间的自相关性很强，互相关性很弱，这说明该矩阵具有类正交性，因此称P’矩阵是一种类正交矩阵。
2．3 组合BCH码的类正交性
对于同组的BCH码，由前面的BCH码的组合特性可知，在同组的素多项式中，如果将其中的t个素多项式组合，得到组合BCH码的码长nt=n =2m-1，阶数mt=tm，信息位长度为k=nt-mt=n-tm，则组合BCH码得到的类正交矩阵P’的大小为：
kt×mt=(n-tm)×tm (10)
由上式可以看出，对于类正交矩阵P’来说，当组合的素多项式的个数越多，即t越大，那么它的行数就越少(n-tm越小)，它的列数就越多(tm越大)。对于类正交矩阵P’中的行向量来说，由于t变大，那么每行的码元个数(每行的码元个数就等于列数)也会增多，随着码元个数的增多，其中“-1”和“1”的个数也趋于平衡，所以行向量之间的类正交性越好，即行向量之间的互相关系数越小；而对于类正交矩阵P’中的列向量来说，t变大使得每列的码元个数(即行数)减少，因此每列中“-1”和“1”的个数的平衡性越差，所以列向量之间的类正交性也越差，即行向量之间的互相关系数变大。
图1，图2是在阶数为8，码长为255的同组中选取不同素多项式进行组合，t=4和t=8时的类正交图。

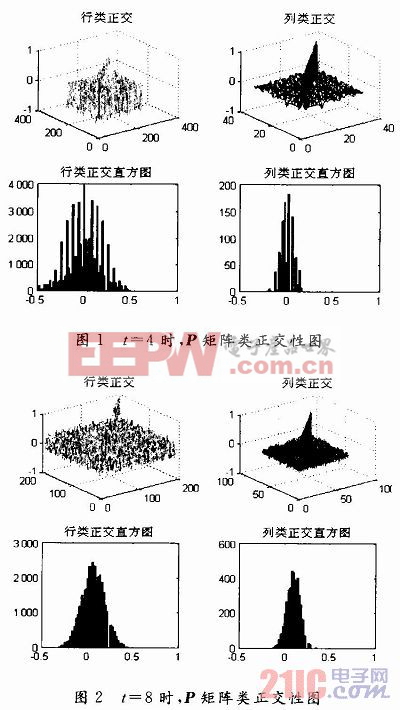
t=4时，行向量的互相关系数小于0．2的占总数的75．88％，列向量的互相关系数小于0．2的占总数的96．68％；t=8时，行向量的互相关系数小于0．2的占总数的84．98％，列向量的互相关系数小于0．2的占总数的93．35％。由此可见，当t越大，行向量之间的类正交性越好，列