标准正交基应用于通信原理课程的教学研究

摘要：通信原理是一门具有很强物理意义的专业理论课，因其内容抽象而繁杂，给教学带来了一定的困难。基于整合教学内容的目的，本文探讨了将众多调制方式(包括模拟调制和数字调制)统一为正交调制模型的教学方案。为了在满足教学要求的前提下降低教学难度，提出了用MATLAB进行仿真演示的教学方法。教学实践证明，该教改方案不仅达到了有效整合课程内容的目的，而且通过使用信息工具将抽象知识具体化、直观化的这一途径使得教学质量得到了提高。
关键词：向量空间；标准正交基；信号空间；调制解调；MATLAB

2009年1月，教育部高教司设立了“利用信息技术工具改造课程”项目，“用MATLAB和建模实践改造工科线性代数课程”是其中一个子项目。而“需求牵引”和“技术推动”正是此项目改革的动力。是的，后续课程的需求是什么?采用MATLAB软件如何增强教学?这是当前线性代数课程教育者必须思考的。
我校作为参与此项目院校之一，教改也取得了显著成果，得到了专家、教师和学生的支持，给予很高的评价，但是如何将线性代数在工科教育中的重要作用进一步发挥出来呢?工科线性代数改革的主要目的不是在于课程自身，而是对后续课程产生辐射，推动各种有关的后续课乃至整个教学计划的改革和现代化。
基于此，本文针对通信原理课程内容杂而多，难教难学的特点，以此课程中调制内容为例，探讨了现有教学中存在的问题，提出了将线性代数中向量空间及标准正交基的知识与调制内容进行深度结合，并将MATLAB运用于教学的解决方案。

1 通信原理课程教学现状
通信原理课程是通信工程、电子信息工程等本科专业的专业基础课。在实际教学中，本科院校一般都是选用国内一些优秀教材，这些教材内容选取大同小异。一般由随机过程、信道与噪声、模拟调制系统、数字基带传输系统、数字频带传输系统、模拟信号的数字传输系统、数字信号的最佳接收、同步原理、差错控制编码这些内容组成。由于其具有很强的理论性、系统性和物理性，内容杂而多，很多学生反映“乱”，而就每一章来说，能听懂，会做题，但没有课程的整体思路。现以调制部分的教学为例，讨论难教难学的原因。原因一，调制方式多、数学表达式多。在大多数通信原理教材中将调制分为两部分，一部分是模拟调制，包括有AM、DSB、SSB、VSB等；另一部分是数字调制，包括有二进制或多进制的ASK、FSK、PSK以及QAM、MSK、GMSK等。不同的调制方式有着不同的数学表达式。尽管在教学中不断强调，不论是模拟调制还是数字调制都是围绕幅度调制、频率调制、相位调制3类基本调制展开的，本质是一样的。但是在理论学习过程中，众多的调制方式、数学表达式仍然让学生感到混乱、难理解。原因二，知识抽象，有很强的物理性。调制在实际中有广泛的应用，但是学生学习这部分常常会感到，即使能将每个调制方式的表达式记住，却不知如何用；题目中已知条件给了不少，却弄不清楚是什么意思；面对实际问题，不知如何分析，如何实现。这些都是南于知识抽象，不理解公式和物理量的物理意义所造成的。如何解决或改善上述两个问题呢?首先，如果能将纷杂的调制方式统一为一个数学模型，换句话说，就是可以用一个通用的数学模型分析所有模拟和数字调制方式，那么可以改善甚至解决第一个问题。其次，如果能将MATLAB用于教学，通过仿真将抽象知识直观化、具体化，那么可以解决上述第二个问题。以下讨论具体解决问题的方案。首先介绍调制方式的数学模型如何统一。

2 调制数学模型的统一
为解决调制方式多，数学表达式繁杂给教学带来的困难，现将线性代数中向量空间和标准正交基概念引入，通过阐述向量空间和信号空间的关系，将标准正交基和通信原理课程中的调制内容结合起来，实现调制方式数学模型的统一。
2．1 向量空间与信号空间的联系
向量空间就是线性代数中一个核心概念。掌握有限维向量空间，将其扩展到信号空间，这一点对于应用数学研究者是非常重要的。
2．1．1 向量空间
根据向量空间定义，可以获知以下信息：1)向量空间是满足某种运算关系的向量的集合：2)在n维向量空间中线性无关的n个向量构成的向量集合就是向量空间的一个基；3)基是生成向量空间的最基本的向量集合，空间中的任意一个向量都可以由基线性组合得到；4)在Euclid空间引入标准正交基对于揭示空间结构、简化表述非常有利。

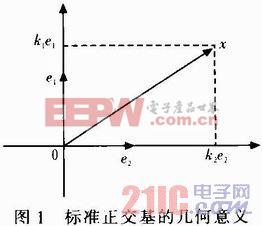
此概念具有非常直观的几何意义。例如在二维向量空间中的体现如图1所示。其中向量e1=[1，0]T，e2=[0，1]T。根据标准正交基的定义可知，