一种分析复杂微波电路的新方法
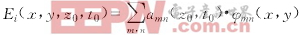 (6)
(6)
其中amn(z0,t0)为第(m,n)次基函数的系数,即幅度,这样从参考面z=z0看入的微波电路可等效为一个基于基函数的等效时域多模电路.基函数的函数形式既可以是适用于一般电路的正交函数形式,也可以是特别适用于某类电路的特殊正交函数.一般说来,当电路几何结构比较复杂,不易根据电路特性选取特殊的正交函数作为基函数时,可以选取矩形脉冲函数(取网格结点的值作为整个网格的平均值,故脉冲宽度为一个网格的宽度).但因脉冲函数描述的只是系统的局部信息,因此要达到足够的精度,函数的展开项数较多.当正交函数可以有效表述电路的全局信息时,通常只需几项或十几项,就可以达到所需的精度.例如,对于均匀填充的矩形波导问题,如根据波导内的场的分布特性,把基函数选为{sin,cos}正交函数集,通常只需5项就可以满足要求.相比较之下,至少需要60个脉冲即60个结点方可较准确地描述波导系统横截面上的空间场分布.
基函数的正交性使得每一个基函数可以被视为一个独立的端口,因此上述基于基函数的等效时域多模电路就可以进一步被视为一个多端口网络.
2.等效多端口网络特性的计算
冲击函数的频谱是无限宽的,因此不能直接使用FDTD算法求解系统的冲击响应函数.FDTD-Diakoptics使用高斯脉冲调制波作为激励,通过加窗Fourier变换技术,求得有限带宽微波电路的冲击响应函数.其中,高斯脉冲激励的调制频率为电路工作频带的中心频率,脉冲宽度和脉冲时间采样间隔取决于频率分辨率和带宽.尽管激励脉冲具有有限带宽导致FDTD-Diakoptics求得的冲击响应函数中包含了加窗带来的影响(称此时的冲击响应函数为准冲击响应函数),但是只要满足下述条件:使用FDTD-Diakoptics分析整个电路特性时,各个子电路使用具有相同频谱特性的激励脉冲,计入加窗对时域脉冲的展宽效应,最终得到的冲击响应函数的频域响应是足够准确的.
五、FDTD-Diakoptics应用实例及讨论
本文以一个波导带通滤波器的特性分析为例说明该算法的应用.图3为一个具有5个膜片的矩形波导带通滤波器(WR34).按照本方法首先将该滤波器分为5个部分,使用FDTD对其进行计算,求出在所有连接参考面处(图中虚线所示)的场分布.FDTD计算中,高斯脉冲调制函数为:f(t)=AmaxA(x,y)exp[-((t-t0)/T)2].sin(2πf0t),其中调制频率f0为WR34-TE10模单模工作频带的中心频率;A(x,y)为激励幅度空间分布,Diakoptics算法中需计算所有可能存在的基函数单一激励时的响应,所以A(x,y)依次选为每一个基函数.激励函数幅度Amax取决于其沿传播方向的衰减及计算精度,基本原则是达到不连续性处和观察面处的场仍具有足够大的幅度.T的取值要保证在激励脉冲的频谱上截止频率点处的能量具有足够小的值.本例中,WR34的单模工作频带为:fTE10=17.369GHz,fTE20=34.738GHz,f0=26.0535GHz,T=200(ps),t0=3T,Amax=10,基函数为φn(x)=sin ,相应的系数an(z0,t)如图4所示(由于文章篇幅原因,只给出一个结果).图5为用本文方法得到的滤波器频率特性,图中可见该结果与FDTD结果吻合很好.
,相应的系数an(z0,t)如图4所示(由于文章篇幅原因,只给出一个结果).图5为用本文方法得到的滤波器频率特性,图中可见该结果与FDTD结果吻合很好.
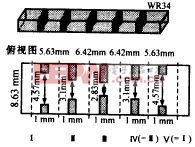
图3 五膜片WR34波导带通滤波器示意图 |
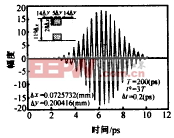
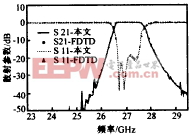
图4 本文方法得到的图3中第一个子电路反射波基函数的系数 | 图5 图3所示WR34波导滤波器的频率特性 |
| 六、结 论 本文介绍了一种分析复杂微波电路的新方法:FDTD-Diakoptics方法,它可克服传统的FDTD方法需要大内存、长计算时间的弊病,并可充分发挥FDTD可易于研究复杂几何结构电路的优势,经作者的若干分析设计实例证明,该方法不但比较灵活,且具有较高的精度,是一种比较有效的微波电路仿真分析方法. |
- GSM/UMTS手机的检验和最终测试方法(09-07)
- 多种Wi-Fi定位方法对比 移动领域选谁(09-17)
- 轻轻松松让你学会阻抗匹配原理和方法(06-28)
- 频谱仪的结构,检定项目和方法(07-04)
- 一种解决FMCW雷达发射机功率泄漏的方法(04-22)
- 基于有限元的螺旋天线设计方法(11-04)
