一种分析复杂微波电路的新方法
,如图1所示.那么如何将Diakoptics算法应用于微波电路特性分析中呢?在介绍这一点之前,本文首先简要介绍Diakoptics算法的数学描述.

图1 媒质中反射和透射现象可以用来形象描述两个微波子电路间的耦合关系 三、Diakoptics算法的数学描述 fr1(t)=gr1(t)+gt2(t)*hr1(t)*gt1(t)+gt2(t)*hr1(t) 使用并行算法,从f电路的输入端口看入的冲击响应函数fr1(t),ft2(t)以及从f电路的输出端口看入的冲击响应函数fr2(t),ft1(t)分别为: fr1(t)=gr1(t)+gt2(t)*hr1(t)*gt1(t)+gt2(t)*hr1(t) 其中,*代表时域卷积,上下标的含义不变. |
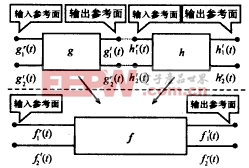
图2 可说明Diakoptics算法的两个子电电路 |
多端口子电路连接时,上述算法依然成立,只是式中各冲击函数应换为相应的子矩阵.例如设g网络为输入端有M个、输出端有N个端口的M+N端口网络,h网络为输入端有N个、输出端有L个端口的N+L端口网络(g与h相邻面的端口数目应相同),g网络输入参考面处的反射、传输子矩阵分别为:

和

式中下标代表参考面,i←j的意思为:i为响应所在参考面,j为激励所在参考面;上标代表端口,m←n的意思为:n为输入端口,m为输出端口.同理,g网络输出参考面处的反射、传输子矩阵分别为:

和

h网络相应子矩阵可用同样方法求得.连接后网络的冲击响应函数[f]为:
[fr1(t)]=[gr1(t)]+[gt2(t)]*[hr1(t)]*[gt1(t)]+[gt2(t)]
*[hr1(t)]*[gr2(t)]*[hr1(t)]*[gt1(t)]+…
[ft2(t)]=[gt2(t)]*[ht2(t)]+[gt2(t)]*[hr1(t)]*[gr2(t)]*[ht2(t)]+…
[fr2(t)]=[hr2(t)]+[ht1(t)]*[gr2(t)]*[ht2(t)]+[ht1(t)]
*[gr2(t)]*[hr1(t)]*[gr2(t)]*[ht2(t)]+…
[ft1(t)]=[ht1(t)]*[gt1(t)]+[ht1(t)]*[gr2(t)]*[hr1(t)]*[gt1(t)]+… (4)
其中[fr1(t)]、[ft1(t)]、[fr2(t)]和[ft2(t)]分别为M×M、L×M、L×L和M×L阶子矩阵.下面以[gt2(t)]*[ht2(t)]为例说明如何计算矩阵卷积,并以[gt2(t)]*[ht2(t)]的第一个元素为例,说明其物理意义:
 (5)
(5)
g1←11←2*h1←11←2:h子网络输出参考面上第一个端口的输入通过gh连接面第1个端口的耦合在g子网络输入参考面上端口1产生的输出;g1←21←2*h2←11←2:h子网络输出参考面上第一个端口的输入通过gh交界面第2个端口的耦合在g子网络输入参考面上端口1产生的输出;g1←N1←2*hN←11←2:h子网络输出参考面上第一个端口的输入通过gh交界面第N个端口的耦合,在g子网络输入参考面上端口1产生的输出;所以[gt2(t)]*[ht2(t)]的第一个元素描述了h网络输出参考面上第一个端口上的输入耦合到g网络输入参考面第一个端口的输出.
四、Diakoptics算法在微波电路分析中的实现
Diakoptics源于网络理论,为将其应用于微波电路的分析中,首先需要建立适于使用Diakoptics方法的微波电路的等效电路模型.
1.微波电路的等效时域网络模型
建立微波电路等效时域网络模型的基本方法是:利用基函数技术(或称时域模技术)将参考面处的场表示为选定的正交基函数的线性组合,将一个微波网络等效为一个多模电路,进而再将多模电路等效为多端口网络的方法.
选定的基函数满足下述条件:只是空间坐标的函数;与时间无关;构成一个完备正交集.且对于给定的微波电路,选定的基函数应能够有效地描述电路中电磁场的分布规律.假设:X-Y平面为电路横截面所在平面,Z为传播方向,电路在Dirac-δ函数激励下在z=z0处的电场分布为Ei(x,y,z0,t),{φmn(x,y)}为基函数族,用φmm(x,y)可将微波电路中t=t0,z=z0处的场表示为:
- GSM/UMTS手机的检验和最终测试方法(09-07)
- 多种Wi-Fi定位方法对比 移动领域选谁(09-17)
- 轻轻松松让你学会阻抗匹配原理和方法(06-28)
- 频谱仪的结构,检定项目和方法(07-04)
- 一种解决FMCW雷达发射机功率泄漏的方法(04-22)
- 基于有限元的螺旋天线设计方法(11-04)
