基于舰船辐射噪声的舰船目标定位技术

ψc(x)的k(k>0)阶导函数表示为ψc(k)(x)，k阶积分函数为ψc(-k)(x)，其中，定义ψ(0)c(x)=ψc(x)(积分下限0可为任意值，但必须固定)。可以得到下式：

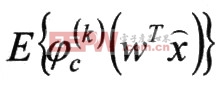这说明，使用可以通过最大化代价函数而由有噪观测数据估计独立分量。这里称统计量为数据的高斯矩。因此，估计有噪ICA模型可以通过对拟白化后的数据x最大化如下的代价函数来实现：

其中X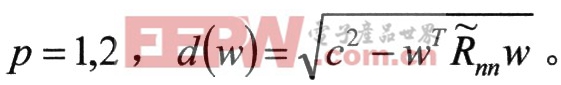对于式(5)进行优化求解，可得到改进形式的定点算法。可将无噪时的所有期望(高斯矩)，由相应的一致估计(有噪数据的高斯矩)代替。因此，可得到拟白化数据的定点迭代的初步形式：

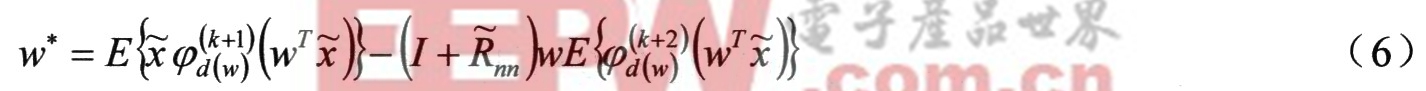
其中w*是w的更新值，在每次迭代后被归一化。在每步迭代之前，调节c使可简化式(6)的算法。最后可得拟白化数据关于偏差消除的定点算法：

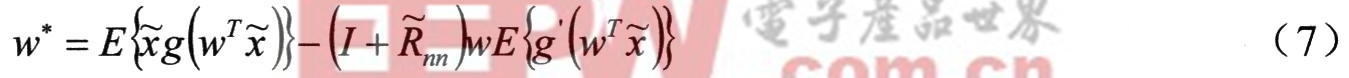
其中w*是w的更新值，在每次迭代后被归一化。上述的公式每次只能得到一个独立分量，使用与无噪时相同的去相关方法，就求得所有的独立分量，从而完成分离工作。
3．2 时差估计
在完成盲分离处理后，就可以得到源信号的恢复形式。相关计算的工作就是估计两组阵列接收源信号之问的延迟△τ。对于同一个辐射源信号，由于到达位置的不同，接收到的时间也不同，这种情况下，就必须在时移中考虑两个信号的相似性，把s2(n)延迟时间τ使之变为s2(n一τ)，考察s2(n)与s2(n一τ)的相似性，即计算其相关系数rs1s2：

当τ从一∞到+∞时，rs1s2(τ)就是τ的一个函数，称rs1s2(τ)为s1(n)与s2(n-τ)的互相关系数，τ为s2(n-τ)的延迟时间，若|rs1s2(τ)|在τ0达到最大值，则τ0为这两个信号的时差即△τ。
3．3 定位计算
假设目标声源T到达阵元S1、S2、S3、S4相对与到达阵元S0的时差分别为τ01，τ02，τ03，τ04，可以得到其定位方程：

c为声速，这里取c=340．29m／s，在直角坐标系中，目标声源T的位置坐标(x,y,z)与球坐标系的位置坐标(r，ψ，θ)的关系式为：

式中0°≤θ≤90°，O°≤ψ≤360°。由式(9)可知，与定位相关的量包括时差τ01，τ02，τ03，τ04，阵元间距D以及声速c有关，由于在一定的阵列和环境中，阵元间距D和声速c相对固定，这里可视为常数，因此定位精度主要取决于时差的估计精度，这里设时差估计精度为dτ。对式(9)求相对时差τ01，τ02，τ03，τ04的偏导，相应估计值的标准偏差可表示为：

由式(11)可知，定位参量估计值与时差估计精度dτ、阵元间距D、声速c、俯仰角θ和目标真实距离r有关，结合式(10)，对定位相关的三个坐标变量求偏导，可得：

定位误差则可表示为：

4 仿真实验
为验证算法的有效性，下面分别就直接相关、广义相关和基于盲分离的直接相关方法进行一系列的实验。由图l建立的接收模型可知，延迟时间为50个采样间隔。接收的主要源信号包括一路舰船实测信号，一路服从α稳定分布的尖峰脉冲噪声，见图2。服从α稳定分布的随机变量如下产生：分别产生两个独立的随即变量V和W，其中，V满足在(一π／2，π／2)范围内均匀分布，W满足均值为l的指数分布。

试验过程如下：首先对接收信号直接进行相关处理，结果如图3的第一排所示，相关易出现多个极值且有偏差，从而使得到的结果并不准确。其次，将接收信号经盲信号处理后的进行处理相关，相关峰非常明显，结果如图3的第二排所示。通过改变噪声的影响，对每个噪声点分别进行了1000次实验，结果(如图4所示)证明：经盲相关处理后对延迟时间估计的结果远比直接进行相关、广义相关方法估计的结果要准确和稳定，达到一定的信噪比后，正确估计的概率几乎为100％，广义相关方法相比直接相关的正确概率有一定的提高，显然还是存在一定的误差。由实验结果可知：在复杂信号环境中，最好的方式是先将信号提取出来再进行相关处理，否则，时差估计的精度和稳定性将很难提高，进而影响定位精度及其稳定性。这里信噪比定义为：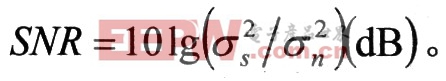

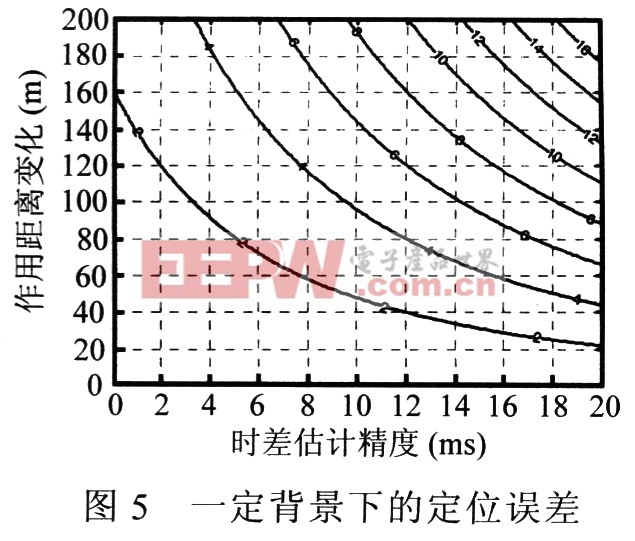
为验证定位性能，分别进行了一系列实验，限于篇幅原因，这里只对其中的一种状况进行说明：设声速c=340．29m／s，俯仰角θ=45°，方位角ψ=30°。在不同的时差估计精度下，当目标真实距离r变化时，对目标的定位精度误差如图5所示。实验结果表明这种定位方法与接收阵元间距、目标真实距离和时差估计精度等都有关系，这与第3部分的分析是一致的，具有一定的指导意义。

5 结束语
本文通过建立的接收模型和定位算法，能够通过对接收的舰船辐射噪声对舰船目标进行定位，在一定程度上可提高水下探测能力。对于不同的舰型，由于舰船噪声的音质节拍、音色及其频谱分布、信号过零点分布等不同，通常可根据这些特征，同时通过本文的盲分离算法处理结果，还可对目标类型进行识别。