有源模拟带通滤波器的设计

滤波器是一种具有频率选择功能的电路，它能使有用的频率信号通过。而同时抑制(或衰减)不需要传送频率范围内的信号。实际工程上常用它来进行信号处理、数据传送和抑制干扰等，目前在通讯、声纳、测控、仪器仪表等领域中有着广泛的应用。

1 滤波器的结构及分类
以往这种滤波电路主要采用无源元件R、L和C组成，60年代以来，集成运放获得迅速发展，由它和R、C组成的有源滤波电路，具有不用电感、体积小、重量轻等优点。此外，由于集成运放的开环电压增益和输入阻抗都很高，输出阻抗比较低，构成有源滤波电路后还具有一定的电压放大和缓冲作用。
通常用频率响应来描述滤波器的特性。对于滤波器的幅频响应，常把能够通过信号的频率范围定义为通带，而把受阻或衰减信号的频率范围称为阻带，通带和阻带的界限频率叫做截止频率。
滤波器在通带内应具有零衰减的幅频响应和线性的相位响应，而在阻带内应具有无限大的幅度衰减。按照通带和阻带的位置分布，滤波器通常分为低通滤波器、高通滤波器、带通滤波器和带阻滤波器。
文中结合实例，介绍了设计一个工作在低频段的二阶有源模拟带通滤波器应该注意的一些问题。

2 二阶有源模拟带通滤波器的设计
2．1 基本参数的设定
二阶有源模拟带通滤波器电路，如图1所示。图中R1、C2组成低通网络，R3、C1组成高通网络，A、Ra、Rb组成了同相比例放大电路，三者共同组成了具有放大作用的二阶有源模拟带通滤波器，以下均简称为二阶带通滤波器。

　

根据图l可导出带通滤波器的传递函数为

式(5)为二阶带通滤波器传递函数典型表达式，其中ω0称为中心角频率。
令s=jω，代入式(4)，可得带通滤波器的频率响应特性为

可画出其幅频响应曲线，如图2所示。图中，当ω=ω0时，电压放大倍数最大。带通滤波器的通频带宽度为BW0.7=ω0／(2πQ)=f0／Q，显然Q值越高，则通频带越窄。

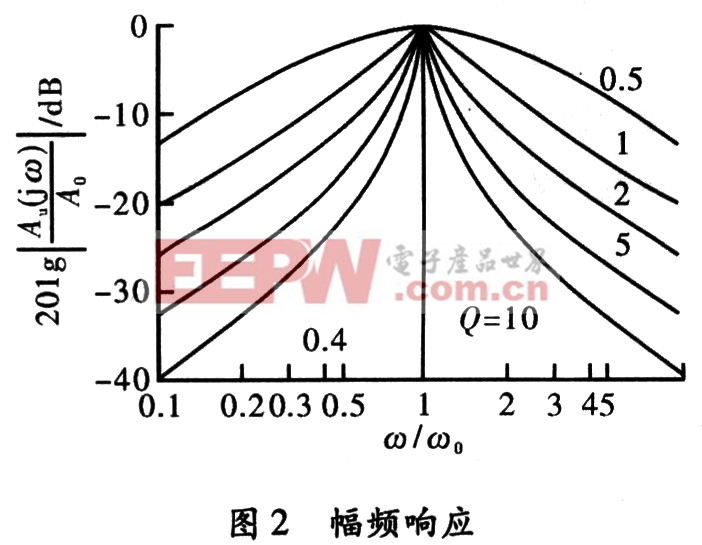
通频带越窄，说明其对频率的选择性就越好，抑制能力也就越强。理想的幅频特性应该是宽度为BW0.7的矩形曲线，如图3(a)所示。在通频带内A(f)是平坦的，而通带外的各种干扰信号却具有无限抑制能力。各种带通滤波器总是力求趋近理想矩形特性。

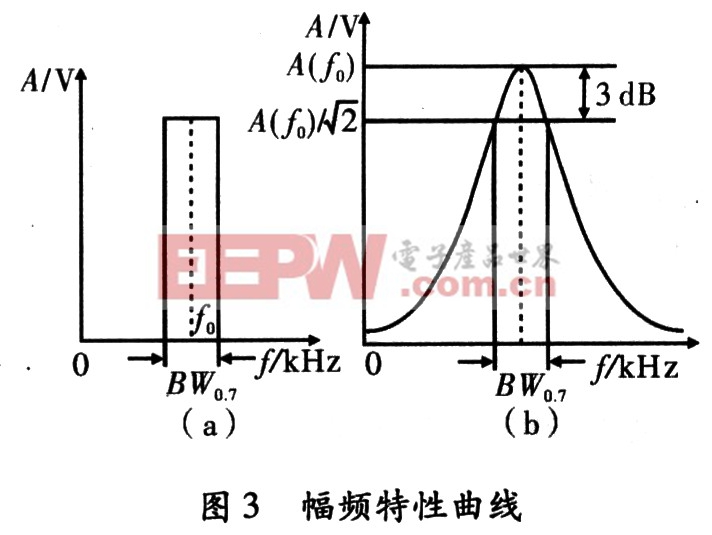
然而实际设计出来的带通滤波器的幅频特性曲线，如图3(b)所示。
在工程上，定义增益自A(f0)下降3 dB(即0．707倍)时的上、下限频率之差值为通频带，用BW0.7表示。要求其值大于有用信号的频谱宽度，保证信号的不失真传输。
综上分析可知：当有源带通滤波器的同相放大倍数变化时，既影响通带增益A0，又影响Q值(进而影响通频带BW0.7)，而中心角频率ω0与通带增益A0无关。
2．2 实际电路设计效果分析
为了能更好的了解二阶带通滤波器在实际电路中应用的效果，设计了如图4的电路进行实验验证。图中U1A部分为放大电路，UlB部分为二阶带通滤波器电路。

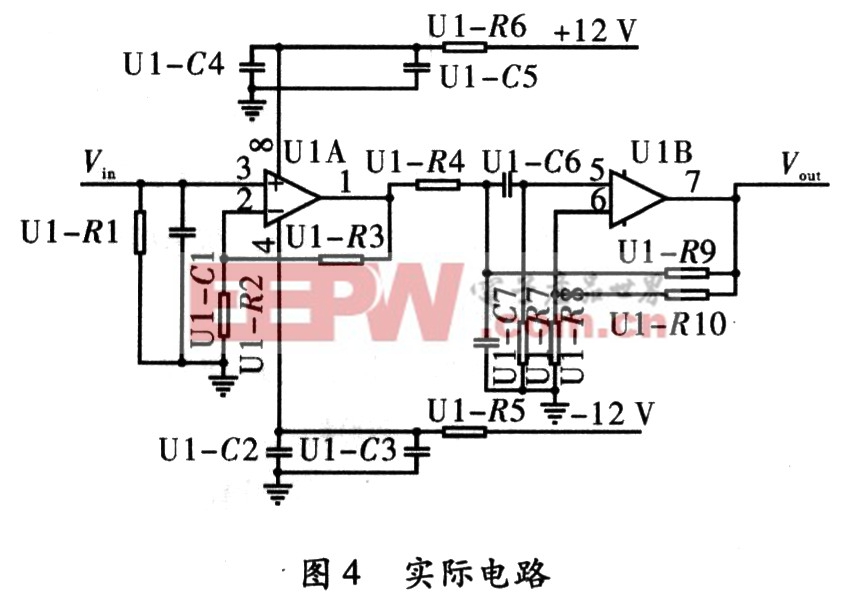
根据式(2)~式(4)，设计出了中心频率在30 kHz附近，品质因素Q为1．55，频带宽度约为19．35 kHz的二阶带通滤波器，并分别对它进行了一级到四级级联所产的电压及频率数据的记录，将记录结果绘制成电压／V~频率／kHz图，如图5所示。

从图5(a)中可以看出，随着级联次数的增加，A(f0)在逐渐变大，BW0.7也在逐渐变窄，说明其对频率的选择性越来越好，对干扰信号的抑制能力也越来越强。
除了级联能增强带通滤波器对频率的选择能力以外，另外，改变品质因素Q值的大小也能达到此效果。众所周知，品质因素Q如果小于0，电路就会自激振荡，无法正常工作。从图2可以看出，Q值越高，则通频带越窄，也就是说滤波器对频率的选择性就越好，对干扰信号的抑制能力也就越强，但并不是Q值越大，电路就越好越稳定。为此，也做了如下实验，即根据式(2)～式(4)，设计出了品质因素Q分别为1．55、2．99、7．87这3种中心频率(理论值)一样的二阶带通滤波器，并分别绘制出了它们的电压/V～频率/kHz图，如图5(b)所示。
从图5(b)中可以发现，品质因素Q值越大，其A(f0)在逐渐变大，BW0.7也在逐渐变窄，但是随着Q值的增加，其中心频率也在向低频端倾斜，并且低频端上升的坡度较陡，相对于低频端，高频端下降的幅度较缓。根据前面的分析也不难看出，Q值如果无限的大，会造成电路的自激振荡，无法正常工作。为了确定这点，也分别测试了Q值为2．99和7．87两种带通滤波器在无信号输入情况下输出端的情况，如图6(a)，图6(b)所示。从两个示波器的图可以看出，Q值越大，其自激的程度也就越大，当Q值达到一定数值时，自激程度与输入信号的强度相当或者比输入信号还要强，就会影响整个电路的正常工作。

2．3 数值的选取
值得注意的是，在设计电路时，首先要根据式(3)确定带通滤波器的中心频率，因为二阶带通滤波器中的元器件比较多，相互干系也比较烦琐。首先确定中心频率对以后的数值计算会有很大的简化。为了方便，也可以取R1=R3=R，C1=C2=C，Ra=Rb=R’，如果想设计一个带放大的带通滤波器，可以根据式(2)或者根据有源带通滤波器的同相放大倍数在确定了其它数值后适当改变Ra和Rb的值得到你想要的放大倍数。这里建议不要随意大幅度改变Ra和Rb的值，因为根据式(4)可以看出在确定了其他数值后改变Ra和Rb会影响Q值，而Q值的大小直接影响到电路的工作状态是否稳定。此外，Q值对元器件数值的大小比较敏感，所以在选择元器件时尽量选取精度较高的器件。