一种脱机手写签名认证方法

1 引言
手写签名认证方法属于生物测定技术。签名认证与其他生物测定技术相比，具有难以模仿、区分性较高、尊重隐私权、信息获取高效等优点，在特征的可搜集性、人体伤害可接受性和鲁棒性方面都很突出，具有广阔的应用前景。但与其他生物测定方法相比，手写签名认证的识别率并不是很高，尤其是脱机中文手写签名认证。因为在脱机签名认证中，丢失了书写过程中的动态信息，使可利用的信息减少，增加了鉴别的难度。另外，有些高超的伪造签名模仿得惟妙惟肖，有时即使是人类专家进行鉴定，识别率也可能会很低。这里针对脱机中文签名，提出一种主成分特征提取和径向基神经网络相结合的脱机手写签名认证方法。

2 主成分特征提取
假设x是一个N×1的随机向量，即x的每个元素xi都是一个随机变量。x的均值可用L个样本向量估计：

而其协方差矩阵可由式(2)估计：

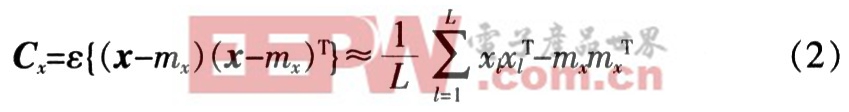
协方差矩阵是N×N的实对称矩阵。对角元素是各个随机变量的方差，非对角元素是它们的协方差。用矩阵A定义一个线性变换，它可由任意向量x通过式(3)得一个新向量y：

式中，A的行向量就是Cx的特征向量。
这里为了方便，对这些行向量按使得其对应的特征值递减的顺序排列。变换后的向量y是具有零均值的随机向量，其协方差矩阵与x的协方差矩阵的关系为：

由于A的行向量是Cx的特征向量，所以Cy是对角阵且其对角元素为Cx的特征值。于是：

从而λk也是Cy的特征值。因为Cy的非对角元素都是零，所以y个元素之间都是不相关的。于是线性变换A去掉了变量间的相关性。此外，λk是第k个变换后的变量yk的方差。可通过略去对应于较小特征值的一个或多个特征向量给y降维。令B为M×N的矩阵(MN)，B是通过丢弃A的下面N-M行，并假定m=0构成的，这样，变换向量变小(即成为M×1维)：

MSE只是与被舍弃的特征向量对应的特征值之和。通常，特征值幅度差别很大，可忽略其中一些较小值而不会引起很大误差。
进行模式分类时．理论上可将一幅MxN图像的M×N个灰度特征作为分类依据，但这样会引起算法运算时间过长而失去意义，系统也因此崩溃。如何对这M×N个灰度特征进行主要特征提取，用提取出的k个灰度特征表征该图像而使算法不会引起很大误差。根据以上论述得知，这样做可行。
对一幅M×N的签名罔像，首先将图像进行局部区域划分，即将图像划分成4×4或者8×8的小块，这样一幅图像就被划分成L个小块，即：

然后将每一个小块的16(或64)个灰度值看成一个N×1的随机变量．假设x是一个N×1的随机向量，x的每一个元素都是用上面的一个小块的16(或64)个灰度值构成的随机变量。实际x是一个16(或64)×L的矩阵，x的协方差矩阵由式(10)估计：

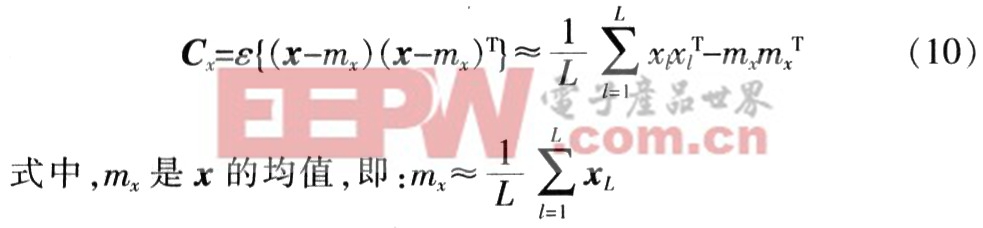
通过求得Cx的特征值来表征图像的灰度主成分特征。将求得的特征值与先前的M×N个灰度特征相比，已明显减少。这里取前10个最大的特征值作为特征分类依据，由于后面的特征值很小，对其忽略不会引起太大误差。

3 径向基函数神经网络及其分类器设计
径向基函数神经网络RBFNN(Radial Basis FunctionNeural Network)起源于数值分析中的多变量插值的径向基函数，它不仅具有任意精度的泛函逼近能力和最优泛函逼近特性，而且具有较快的收敛速度。这里利用径向基函数神经网络构成一个分类器实现签名真伪的认证采用高斯核函数作为径向基函数，形式为：

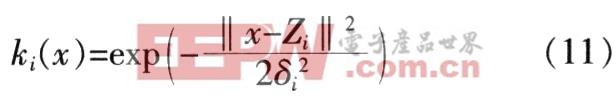
式中，Zi是核函数的中心，δi为核函数的宽度，可控制基函数的径向作用范围，即方差。
而第i个隐结点的输出定义为：

式中，wi是第i个隐结点到输出层结点的权值，θ是输出层结点的阈值。
一般常利用K均值聚类算法确定各基函数中心及相应的方差，网络权值的确定用局部梯度下降法修正。由于K均值聚类方法要事先给出聚类个数K，且聚类结果对K 值大小都很敏感，不同K值的聚类学习结果往往大相径庭，因此，如何确定K值是一个难题。这里不采用上述的K均值聚类方法，而采用文献[4]中的一种根据相似性阈值和最小距离原则的简单聚类方法确定RBF网络的中心。其主要步骤为：
(1)设待分类的模式集为{x1，x2…xn}，选定类内距离门限T；
(2)seed=RandomSelect(x)；∥从对象集合x中，任选一对象Seed；

(3)Dist1，2=Compute Distance(seed,x2)；∥计算下一模式特征矢量x2到Seed的距离；
(4)若Dist1，2>T，则建立新的一类ω2，其中心Z2=x2，若Dist1，2≤T,则x2∈ω1；
(5)假设已有聚类中心Z1?Z2…Zk，计算尚未确定类别的特征矢量xi到各聚类中心Zj(j=1，2…，k)的距离dij。如果dij>T，则 xi作为新的一类ωk+1的中心，Zk+1=xi，否则，如果dij=mindij，则判断xi∈ωg,检查是否所有的模式都划分完类别，如都划分完则结束，否则返同(5)，
上述算法采用规格化的Euclidean计算公式度量两个对象间的距离。具体公式定义如下：