一种基于小波域的分形图像编码改进算法

(1) 首先对图像进行多次小波变换，产生各个子带图像。通过对图像行、列相关性的计算分析，确定各子带小波域图像分割的形状。为了保证信噪比，对最低分辨率的子带图像LL1、HL1、LH1、HH1不编码。
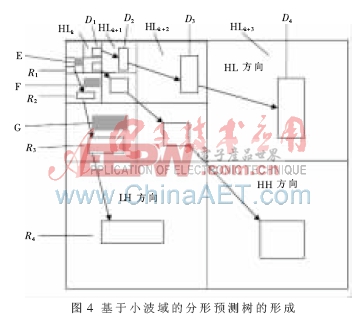
(2) 同时在水平、垂直、对角线3个方向上形成一棵一棵图像树，即零树。如LH方向上的R=(R₁，R₂，R₃，R₄）就是其中一棵图像树，而D=(D₁，D₂，D₃，D₄)表示HL方向上的相似树。然后在LH1中寻找与图像块R2最佳分形匹配的代表块E1，再由E1按照零树结构产生一棵代表树E=(E₁，E₂，E₃)。同理，在LH2中寻找与图像块R3最佳分形匹配的代表块F₂，并生成代表树F=(F₁，F₂，F₃)。在LH3中寻找与图像块R4最佳分形匹配的代表块G3，并生成代表树G=(G₁，G₂，G₃)。
(3)分别计算图像树R与3棵代表树E、F、G的距离，距离最小的代表树就是图像树R的预测树。然后将预测树在相应层次的位置以及经历的几何变换和仿射变换作为图像树R的分形预测编码。
(4) HL、HH方向按同样方式编码,只是构成的R块和D块的形状大小不同。这样，在改进算法中,编码只需对代表树中的一个代表块进行分形编码。而解码时，又可依据这个代表块通过零树结构推出其他代表块，再分形预测图像块R。
由于前面针对小波分解图的能量分配特性已经采用了非均匀的分形块形状的选取，再结合这种分形预测编码方法，其结果大大提高了分形编码的速度，缩短了编码时间，在提高压缩比方面也取得了良好的效果。
3 实验结果
　实验采用图1所示图像，分别用基本分形编码方法和本文的改进算法进行实验，其重建图像如图5所示。基本分形编码时各子图中图像块大小为4×4，相似块大小为8×8，改进算法中对小波分解图像块的分割方法如图2所示，相似块大小取为图像块大小的2×2倍，实验结果如表1所示。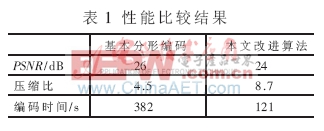

　本文提出基于小波域的分形图像编码改进算法是将小波域分形与分形预测方法相结合，由表1可知，与基本分形算法相比，在恢复图像质量接近的情况下，压缩比提高约2倍，信噪比下降2 dB，而编码时间大大缩短，提高了编码速度，表明在提高压缩比方面，效果良好。
参考文献
[1] 余松煜，张文军，孙军.现代图像信息压缩技术[Ml.北京:科学出版社，1998.
[2] 陈守吉，张立明.分形与图像压缩[M].上海：上海科技教育出版社，1998.
[3] BRENDT W，GERHARD D J. A review of the fractal image coding literature[J]. IEEE Transactions on Image Processing, 1999, 8(12):1716-1729.
[4] RINALDO R, CALVAGNO G. Image coding by block prediction of multiresolution subimages[J]. IEEE Transaction On Image Processing ,1995, IP-4(7):909-920.
[5] DAVIS G. A wavelet-based analysis of fractal image compression[J]. IEEE Transactions on Image Processing, 1998,7(2):141-154.
[6] DAVIS G. Adaptive self-quantization of wavelet subtrees: a wavelet-based theory of fractal images compression[C]. SPIE Conf. on Mathematical Imaging: Wavelet application in Signal and Image Processing, San Diego:1995:265-279.
[7] WALLE A V D. Merging fractal image compression and wavelet transform methods[C]. In Fractal Image Coding Analysis: A NATO Series Book, Yuval Fisher, Ed. New York: Springer Verlag,1996:523-597.
[8] KRUPNIK H, MALAH D, KARNIN E. Fractal representation of images via the discrete wavelet transform[C]. In IEEE 18th Conference of EE, Israel: 1995,3:187-191.
[9] 张宗念，马义德，余英林.基于方向性零树小波的分形图像编码[J]．电子科学学刊，2000，22(5):780-783.
[10] 周艳， 吴敏金.基于方向剖分的小波域分形图像压缩[J]．华东师范大学学报（自然科学版），2002，3(9)：20-23.
[11] 谢鑫，马争鸣.基于小波系数零树结构的分形预测图像编码[J].中国图像图形学报，2000，5（11）：920-924.
[12] JACQUIN A E. Fractal image coding: A Review[J]. Proc. of IEEE, 1993, 81(10):1451-1465.