为您的转换器选择正确的时钟(1)
许多系统中,目标信号可分散在5 MHz或更高频率上。某一路径上的延迟会在整个频谱上引入频率相关相位延迟。 幸运的是,该延迟是线性相位延迟,可以用多种方式进行校正。不过,必须了解时钟或模拟路径内的延迟是如何导致额外相位变化的。时钟和模拟路径之间的差分延迟会随频率变化产生相位误差,计算公式如下: 如上所示,这是与频率成函数关系的线性延迟。通常,线性相位延迟无需担心,除非有多条路径正在进行匹配,如相控阵或MIMO(多输入多输出)系统。即便如此,只要路径间的误差相互匹配,也不会造成问题。当延迟以非线性方式随频率变化时,问题就出现了。群延迟是衡量不同频率的信号在给定路径中的传播速率的指标。由于延迟变化,相移不同于线性相位,难以进行校正。群延迟通常更多地与滤波器路径而不是系统时钟相关,因此不在本文讨论范围之内。 时钟纯度 了解时钟纯度十分重要。关于这一问题,有许多应用笔记可供参考,如本文参考文献部分所列出的笔记。时钟纯度涉及几个基本成分,其中包括宽带抖动和宽带相位噪声。虽然此处予以单独考虑,但它们在真实应用中具有组合效应。 采样过程在时域中是一个乘法过程,因此在频域中是一个卷积过程,就像混频器。我们来看看采样过程。模拟输入在时间上是连续的,虽然这一点是显而易见的,但采样时钟(尽管可能来源于正弦曲线)最终却是用于在编码信号过零处以等幅、有限持续时间的假定单位脉冲驱动样桥。该过程的结果是将该单位脉冲与时域中的模拟输入相乘,也即频域中的卷积。 在图4示例中,x(t)表示连续时间模拟输入波形,p(t)表示理想采样函数,xp(t)表示采样输出。 利用这些项,可将输出样本表示为: 其中 : 在频域中,该公式可表示为: 由于p(t)为时域中的脉冲序列,因此同时也是频域中的脉冲序列,表示为: 将上式代入前面的公式可得: 该公式显示,采样模拟输入频谱以采样速率ws的整数倍无限重复。 该关系既适用于宽带噪声也适用于杂散,因此在考虑时钟对采样过程的效果时很有用。 (未完待续)
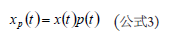
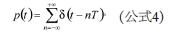
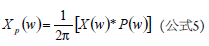
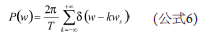
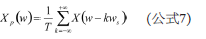
转换器 ADC 时钟 201106 201105 相关文章:
- RS-232至RS-485RS-422接口的智能转换器(01-24)
- 同步降压转换器电路设计基础(01-01)
- 真有效值AC/DC转换器AD736及其在RMS仪表电路中的应用(02-16)
- 满足FPGA电源设计需求的DC/DC转换器(02-15)
- 开关DC-DC转换器的EMI方案(04-29)
- 多媒体手机的电源管理方案(04-26)
