二进制数及其他

1。采用这种方法，我们就可以用有限的数码来表示无限的数据了。

总结一下，十进制采用了 0，1，2，3，4，5，6，7，8，9 共 10 个数码，基数是 10，进行运算 的时候，我们采用逢十进一。

这是我们现实生活中需要用到的十进制的一些情况，那么我们在数字电路中必然也要采用这种计数方 法，电路中传输的就是电压和电流，我们要用 10 种不同的状态来表示这 10 个数码有点困难。我们举例来 说吧，譬如有一个电压，0～5V ，那么我们就可以这样来表示 0～9 这 10 个数码，如表 1。

表 1 电压和数码之间的对应关系

接下来就是要制造一个能够精确的实现 0V，0.5V，1V，1.5V……4.5V 等各种电平的基本电路，但这一

件是非常困难的事情。两个相邻的电平只有 0.5V，电路受到干扰，电平偏移 0.5V，那么就变成另外一个数 据了，而要保证电平完全没有漂移是不可能的，所以，十进制数在电路中很难直接实现了。即使勉强实现 了，数据传输的时候又遇到了更大的数据准确性的问题，因为电平经过导线传输的时候会变化，相邻的两个 电平很容易混淆。这种十进制数在数字电路中是没法直接实现，更别说是在微处理器这种高频电路中实现 了。这样必然要另外想办法了。而戈特弗里德·威廉·凡·莱布尼茨（Gottfried Wilhelm von Leibniz，1646

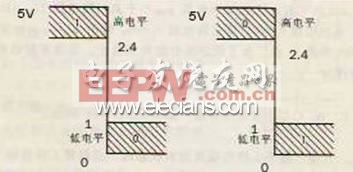
年 7 月 1 日～1716 年 11 月 14 日）在 18 世纪初提出的二进制帮助人们解决了问题，虽然莱布尼茨受中 国的易经八卦启发而发明的二进制数最初不是用来设计电路的，因为那个时候人们才开始研究电的现象，电 灯，电池等都还没有出现。但 20 世纪初人们制造出二极管、三极管、集成电路等的时候，却把二进制拿来 用于电路的设计。二进制数因为只有两个数 0 和 1，状态也只有两种，在电路中实现起来就方便的多了，只 要一个高电平和低电平就可以，甚至说有电流和无电流、有电荷和无电荷都可以表示，这样的话电路的实现 非常简单，而且这种电路也不容易受到干扰，抗干扰性好的多。还是以上面 0～5V 的一个电平来说明，看图2。

从图 2 中可以看到，我们可以认为 0～1V 都是低电平，2.4V～5V 都是高电平，若假设低电平代表 0，高电 平代表 1，那么我们就实现了二进制数了，这个电路简单，而且易与实现，电平允许有一定的漂移，提高了 抗干扰能力，数据传输可*性高的多。所以数字电路中采用了二进制数。

假若以高电平代表 1，低电平代表 0，则称为正逻辑系统，反之，以高电平代表 0，低电平代表 1，

则称为负逻辑系统，一般来说，我们采用正逻辑系统。

2.2 二进制数与十进制数

接下来我们就研究一下二进制数，注意了，下面我们纯粹的研究二进制数，跟二进制的数字电路实现 没有任何的关系了。

借助于十进制数的思路，我们的二进制数有两个数码：0 和 1，基数是 2，进行运算的时候是逢二进 一。举例来说明，比如二进制数 10110（注意，读这个数据的时候只需要把每一位数据读出来就可以了，

千万不要采用十进制数的读法。即这个数读作：一 零 一 一 零，而不是一万零一百一 十，若按照十进制数

的读法，会让别人笑话的。切记切记）。对于这个数，我们知道它的每一位都有权，而且权是 2 的幂，即

10110 ＝ 1X24 0X23 1X22 1X21 0X20 若我们把这些数字相加计算出数值来，就会发现它是一个 十进制数 22，这样我们就把一个二进制数转换为十进制数了。我们接下来就讲二进制数和十进制数的相互

转换问题。

随便拿出一本教材来，关于二进制数和十进制数的相互转换，都讲了一个方法：二进制数转换为十进 制数采用加权法，就是上面说的例子。而十进制数转换为二进制数则分为整数部分和小数部分分别转换，整 数部分用除 2 取余法，小数部分采用乘 2 取整法，然后要列竖式来求解。一般来说，我们在进行应用的时 候，譬如数字电路，单片机中使用的数字都是整数，而且只需要我们快速的计算出这个数据即可，若按照除

2 取余法来求解，则太费时间，这里我讲一种方法，命名为“8421”法，可以快速的求解 255 以内的数据

（超过 255 的数据建议大家用计算器来求解，手算或者心算就太费劲了。）。这个方法就是利用权，一个 4

位的二进制数，它的每一位的权恰好是 8421，如图 3。

128 64 32 16 8 4 2 1

图 3 二进制数每一位的权

接下来我们就以一个具体的例子来说明这种方法的使用。先看二进制数转换为十进制数的例子，就是 上面说的 10110 吧，把它的每一位的权都标出来，