旋转目标干涉逆合成孔径三维成像技术
旋转目标干涉逆合成孔径三维成像技术
本文根据旋转目标微波成像原理,导出了采用干涉逆合成孔径(INISAR)处理获取第三维高程信息的旋转目标INISAR三维成像技术.这种技术通过鉴别由俯仰角微小差异的两副天线分别获取的两幅相位相干的二维图像对应散射中心的相位变化来确定散射中心在竖直维的位置;散射中心的横坐标、纵坐标及幅度由一幅二维图像给出.模拟计算与飞机模型实验测量均得到满意结果.
关键词:雷达目标;微波成像;测量
INISAR 3-D Imaging Technique for Rotating Targets
XIAO Zhi-he,DAI Chao-ming,CHAO Zeng-ming,XU Xiao-jian
(Beijing Institute of Environmental Features,Beijing 100854,China)
Abstract:Based on the principle of microwave imaging of the rotating targets,an INISAR (ISAR Interferometry) 3-D imaging technique of rotating targets is described in this paper.The vertical position of scattering centers are given by comparing their phase difference of two phase coherent 2-D images which are obtained by using two antennas with a little change in pitch angle.The down-range and cross-range position and amplitude of scattering centers of the 3-D image are given by one 2-D image.The simulated and measured results are all satisfactory.
Key words:radar targets;microwave imaging;measurement
一、引 言
雷达目标二维成像的理论和测量技术已经取得了巨大的发展和广泛应用,并成为电磁散射实验室、目标特性及其控制研究、微波遥感等领域不可缺少的标志性技术.作为二维成像的推广,能获取复杂目标散射中心三维分布的三维成像技术,由于要求获取巨大数量的测量数据,从目前的试验手段而言可能需要几十个小时,实际难以实现.因此,完全意义上的三维成像一直未能在实验室中实现.如何采用新的可行的技术途径获得散射中心高程坐标是人们一直试图解决的问题.
干涉图样可以用来捕捉目标表面相对参考平面的位移和变形,这在光学领域已有悠久历史.随着合成孔径雷达(SAR)在微波遥感领域的发展和应用,到九十年代初,人们提出并研究了干涉合成孔径雷达(INSAR)[1~4].INSAR法即通过测量在高度方向上位置有微小差别的两副天线的相位差或是多轨道(可以非同时)情况下测得的相位差,提取有关地形的第三维高程信息.
旋转目标二维成像基于圆周孔径的ISAR成像,通过宽带脉冲压缩得到径向高分辨;通过圆周合成孔径得到横向高分辨.本文根据旋转目标微波成像原理,导出了采用干涉逆合成孔径(INISAR)处理获取第三维高程信息的INISAR三维成像技术.这种技术通过鉴别由俯仰角微小差异的两副天线所获取的相位相干的两幅二维图像对应散射中心的相位变化来确定散射中心在竖直维的位置,从而得到目标散射中心三维坐标.这种技术适用于在同一径向、横向分辨单元内只有一个强散射源的情况.
二、旋转目标二维成像原理
图1为转台逆合成孔径成像的几何关系,其中X—轴为横向,Y—轴为径向.设目标散射中心空域分布为g(x,y),则相参雷达的接收数据(谱域)为:
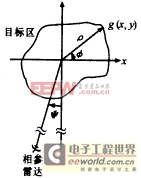
图1 转台成像几何图 G(K,ψ)=∫∫g(x,y)ej2πK(ycosψ+xsinψ)dxdy (1) 式中:K=2/λ,为空间频率,ψ为雷达视线与Y轴(径向坐标)夹角.
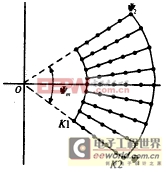
图2 极坐标格栅数据 根据式(1)得到目标二维散射中心分布的估计值
三、INISAR三维成像原理 |
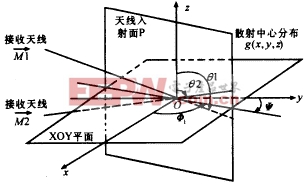
图3 三维成像的几何关系图
并记g的方向矢量为: g=(sinθcosφ,sinθsinφ,cosθ). 设INISAR的两副接收天线分别为M1和M2,均指向目标坐标原点;其入射线均位于包含Z轴在内的入射内平面P内,P与XOY平面交线的方向角为φ1.设M1的方向矢量为 M1=(sinθ1cosφ1,sinθ1sinφ1,cosθ1) (4) M2的方向矢量为: M2=(sinθ2cosφ1,sinθ2sinφ1,cosθ2) (5) 则目标散射中心g在M1和M2上的投影分别为: R1=ρg.M1=xsinθ1cosφ1+ysinθ1sinφ1+zcosθ1 设目标ISAR成像的旋转面为XOY平面,且M1在XOY平面上,M2与XOY平面有夹角Δθ |
- 12位串行A/D转换器MAX187的应用(10-06)
- AGC中频放大器设计(下)(10-07)
- 低功耗、3V工作电压、精度0.05% 的A/D变换器(10-09)
- PIC16C5X单片机睡眠状态的键唤醒方法(11-16)
- 用简化方法对高可用性系统中的电源进行数字化管理(10-02)
- 利用GM6801实现智能快速充电器设计(11-20)

 (2)
(2)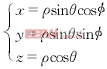 (3)
(3)