基于ADUC7026的PID算法在基站功率控制中的应用

算结果和可调衰减器的传递函数决定，下面介绍两种不同PID算法的流程、程序实现及其测试结果。

　　4.1 位置式PID算法流程

　　图4 位置式PID算法流程图

　　对应图4算法流程图，PID控制部分实现程序如下：

　　ActualOutputPower = 25*(float)ADCForwardPowerResult/1024-43;

　　Error = SetOutputPower - ActualOutputPower;

　　SumError += Error;

　　Output = Proportion*Error + Integral*SumError + Derivative* (Error – LastError);

　　LastError = Error;

　　DACVoltageValue = (float)((Output + 26.1667)*3/31);

　　SetDACValue = (unsigned int)(DACVoltageValue*4096/2.5);

　　这里，DACVoltageValue的值由输入信号功率，两级固定增益放大器和可调衰减器的传递函数决定，实际程序中给出的参数是经系统线性校正后的参数。理想情况下，假设可调衰减器的传递函数为：衰减量=k*控制电压+b，输入信号功率为pin两级固定增益放大器的增益为g1和g2，则DAC的输出应为式(7)所示。

(7)

　　图5所示为采用位置式PID算法，在系统输出功率为-1dBm时，调整其输出功率为-10dBm的实测曲线。

　　图5 改变期望输出功率后的变化曲线(位置式PID算法)

4.2 增量式PID算法流程

　　图6 增量式PID算法流程图

　　对应图6算法流程图，PID控制部分实现程序如下：

　　ActualOutputPower = 25*(float)ADCForwardPowerResult/1024-43;

　　Error = SetOutputPower - ActualOutputPower;

　　DeltaAttenuation = Proportion*(Error-LastError) + Integral*Error +

　　Derivative*(Error-2*LastError + PrevError);

　　Attenuation = DeltaAttenuation + LastAttenuation;

　　DACVoltageValue = (float)(Attenuation*3/31 + 3.887);

　　SetDACValue = (unsigned int)(DACVoltageValue*4096/2.5);

　　PrevError = LastError;

　　LastError = Error;

　　LastAttenuation = Attenuation;

　　这里，DACVoltageValue的值由可调衰减器的传递函数决定，实际程序中给出的参数是经系统线性校正后的参数。理想情况下，假设可调衰减器的传递函数为：衰减量=k*控制电压+b，则DAC的输出应为式(8)所示。

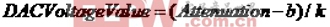
(8)

　　图7所示为采用增量式PID算法，在系统输出功率为-1dBm时，调整其输出功率为-10dBm的实测曲线。

　　图7 改变期望输出功率后的变化曲线(增量式PID算法)

　　5.结论

　　由前面的测试结果可见，在同样的测试条件下，采用位置式PID算法的时候会出现过冲的情况，增量式控制虽然只是算法上作了一点改进，却避免了这种情况的发生。且由于计算机输出增量，所以误动作时影响小，必要时可用逻辑判断的方法去掉。算式中不需要累加，控制增量 的确定仅与最近几次的采样值有关，所以较容易通过加权处理而获得比较好的控制效果。因此，建议采用增量式PID算法来实现基站功率的稳定控制。