自动控制系统的设计--控制系统设计的基本思路

如前所述，一个单输入单输出的控制系统一般可化为图6－1的形式，G0(s)是控制系统的不可变部分，即被控对象，H(s)为反馈环节。未校正前，系统不一定能达到理想的控制要求，因此有必要根据希望的性能要求进行重新设计。在进行系统设计时，应考虑如下几个方面的问题：

（1） 综合考虑控制系统的经济指标和技术指标，这是在系统设计中必须要考虑的。

（2） 控制系统结构的选择。对单输入、单输出系统，一般有四种结构可供选择：前馈校正、串联校正、反馈校正和复合校正，其框图如图6－2。考虑到串联校正比较经济，易于实现，且设计简单，在实际应用中大多采用此校正方法，因此本章只讨论串联校正，典型的校正装置有超前校正、滞后校正、滞后－超前校正和PID校正等装置。

（3） 控制器或校正装置的选择。校正装置的物理器件可以有电气的、机械的、液压的和气动的等形式，选择的一般原则是根据系统本身结构的特点、信号的性质和设计者的经验，并综合经济指标和技术指标进行选择。本书我们以电气校正装置作为控制器，详述有源和无源装置的工作原理和设计方法。其思想方法同样适用于其它类型的校正装置设计。

（4） 校正手段或校正方法的选择。究竟采用时域还是频域方法，须根据控制系统性能指标的表达方式选择。控制系统的性能指标通常包括动态和静态两个方面。动态性能指标用于反应控制系统的瞬态响应情况，它一般可用时域性能指标和频域指标两个方面：1）时域性能指标：调整时间ts 、上升时间tr 、峰值时间tp 和最大超调量
Mp等；2）频域性能指标：开环指标包括相位裕量γ 、增益裕量Ag ；闭环指标包括谐振峰值Mr 、谐振频率ωr 和频带宽度ωb等。

在进行系统设计时，若所使用的指标是时域指标，则一般宜用根轨迹法进行设计，使闭环系统的极点重新配置；若所使用的指标是频域指标，宜用频率法（如伯德图或极坐标）进行设计。

最后需要指出，由于电子技术和计算机技术的发展，目前实际系统中大量采用的控制器是有源校正装置，如典型的PID调节器，但正如下文大家将看到的，无源校正与有源校正尽管组成形式有差别，但它们的工作原理是相同的。

（一）超前校正装置

图6－3分别为无源和有源超前校正网络。对于无源校正装置(a)，忽略该网络的输入阻抗和输出阻抗效应，则其传递函数为：

(6-1)

式中，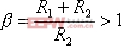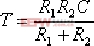

,

上式另一常见形式可写作：

(6-2)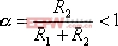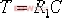

式中，

,

对于有源校正装置(b)，其对应的传递函数为：

(6-3)

式中，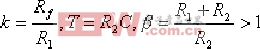

。

负号是因为采用了负反馈的运算放大器，再串联一只反相运算放大器即可消除负号。

在式（6－3）中，令R1C=T1,R2C=T2 ，则（6－3）可写成如下形式：

(6-4)

上式即为实际的比例微分控制器（PD）的传递函数的表达式。

超前校正装置的零、极点分布如图6－4所示，由于β>1 ，故 Gc(s)的零点总在其极点的右侧。由式（6－1）和式（6－2）可知，在采用超前校正网络时，系统的开环增益会有1/β （或k ）倍的衰减。对此，用放大倍数β 或（1/k）的附加放大器予以补偿。经补偿后，令α=1/β ，其传递函数 ，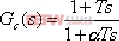

频率特性为:

(6-5)

与式（6－5）对应的幅频特性的表达式分别为：

(6-6)

(6-7)

其相应的极坐标如图6－5。由图可见，超前校正装置的极坐标是一个位于第一象限的半圆，圆心坐标 [(1+1/α)/2,j0],半径为 (1/α-1)/2,从坐标原点到半圆作切线，它与正实轴的夹角即为该校正装置的最大超前角φm ，且有：

(6-8)

此最大超前角对应的频率可由式（6－7）得到。令dφ(ω)/dω=0,则有：

(6-9)

对式（6－6）的幅频特性取对数坐标，有：

根据式（6—7）、