控制系统的时域分析法--控制系统的稳态误差

…被定义为动态误差系数。对N型系统的动态误差系数由下式给出：

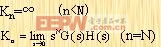其中
K1=动态位置误差系数；
K2=动态速度误差系数；
K3=动态加速度误差系数。

需要说明的是，在一个给定系统中，动态误差系数是与静态误差系数有关的。例如：设下列具有单位反馈的0型系统：

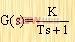其静态位置误差系数、静态速度误差系数和静态加速度误差系数分别是

其中
Kp=K
Kv=0
Ka=0

由于E(s)/R(s)可展开成

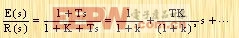所以，依据静态误差系数给出的动态误差系数如下：
k1=1+K=1+Kp

动态速度误差系数由下式给出：

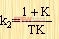当E(s)写成下面的形式时：
E(s)= R(s)+ sR(s)+ s2R(s)+…

动态误差系数的优点就更为清楚。这个级数的收敛域是s=0的邻域，这相当于在时域内的t=∞。假定所有的初始条件为零，并且忽略掉在t=0的邻域，这相当于在时域内的t=∞。假定所有的初始条件为零，并且忽略掉在t=0时的脉冲，则对应的时间解（即稳态误差）由下式求出：

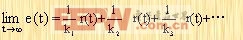这样，由输入函数和它的导数所引起的稳态误差能根据动态误差系数求出，这便是动态误差系数的一个优点。

如果E(s)/R(s)围绕原点展开成一个幂级数，级数的逐项系数就表示系统在缓慢变化的输入作用下的动态误差。动态误差系数是计算任意输入作用下的误差信号和稳态误差的简便方法。用这个方法就不需要实际去解系统的微分方程。

例3-9

设前向传递函数为G(s)= 的单位反馈控制系统，求出它的动态误差系数。还要求出当输入量为r(t)=a0+a1t+a2t2时的稳态误差。

对于该系统 = =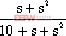0.1s+0.09s2-0.019s3+…

即 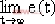=0.1 (t)+0.09 (t)-0.019 (t)+…

则动态误差系数是 k1=∞

k2=1/0.1=10

k3=1/0.09=11.1

由于r(t)由下式给出：r(t)=a0+a1t+a2t²

得(t)=a1+a2t，(t)=2a2，(t)=0

于是，稳态误差为

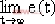= [0.1(a1+a2t)+0.09(2a2)]= (0.1a1+0.18a2+0.2a2t)

只要不是a2=0，稳态误差就变为无穷大。

由以上分析可知，如果E(s)/R(s)围绕原点展开成一个幂级数，级数的逐项系数就表示系统在缓慢变化的输入作用下的动态误差。动态误差系数是计算任意输入作用下的误差信号和稳态误差的简便方法。用这个方法就不需要实际去解系统的微分方程。