3.7.1 线性系统的MATLAB表示
系统的传递函数用两个数组来表示。考虑下列系统: 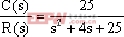 | (3-17) |
该系统可以表示为两个数组,每一个数组由相应的多项式系数组成,并且以s的降幂排列如下:
num=[0 0 25]
den=[1 4 25]
注意,必要时需补加数字零。 如果已知num和den(即闭环传递函数的分子和分母),则命令step(num,den),step(num,den,t) 将会产生出单位阶跃响应图(在阶跃命令中,t为用户指定时间)。 当阶跃命令的左端含有变量时,如:[y,x,t]=step(num,den,t)显示屏上不会显示出响应曲线。因此,必须利用plot命令去查看响应曲线。矩阵y和x分别包含系统在计算时间点t求出的输出响应和状态响应(y的列数与输出量数相同,每一行对应一个相应的时间t单元。x的列数与状态数相同,每一行对应一个相应的时间t单元)。 3.7.2传递函数系统单位阶跃响应的求法 下面讨论由方程(3-17)描述的系统的单位阶跃响应。MATLAB Program3-1将给出该系统的单位阶跃响应曲线。该单位阶跃响应曲线如图3-13所示。 其源程序为: MATLAB Program 3-1
num=[0 0 25];
den=[1 4 25];
step(num,den)
grid
title('Unit-Step Response of G(s)=25/(s^2+4s+25)') 3.7.3在图形屏幕上书写文本 为了在图形屏幕上书写文本,例如,可以输入下列语句:
text(3.4, -0.06, 'Y1')
和
text(3.4, 1.4, 'Y2') 第一个语句告诉计算机,在坐标点x=3.4,y=-0.06上写出"Y1"。类似地,第二个语句告诉计算机,在坐标点x=3.4,y=1.4上写出"Y1"。 3.7.4脉冲响应 利用下列MATLAB命令中的一种命令,可以得到控制系统的单位脉冲响应:
impulse(num,den)
[y,x,t]=impulse(num,den)
[y,x,t]=impulse(num,den,t) 例3-11 试求下列系统的单位脉冲响应: 。MATLAB Program3-2将产生脉冲响应。由此得到的单位脉冲响应曲线如图3-14所示。 其源程序为: MATLAB Program 3-2 num=[0 0 1]; den=[1 0.2 1]; impulse(num,den); grid title(‘Unit-Impulse Response of G(s)=1/(s^2+0.2s+1)’) 3.7.5求脉冲响应的另一种方法 当初始条件为零时,G(s)的单位脉冲响应与sG(s)的单位阶跃响应相同。
考虑上例中讨论过的系统的单位脉冲响应。因为对于单位脉冲输入量,R(s)=1,所以 因此,可以将G(s)的单位脉冲响应变换成sG(s)的单位阶跃响应。 如果向MATLAB输入下列num和den:
num=[0 1 0]
den=[1 0.2 1]
利用在MATLAB Program3-2中给出的阶跃响应命令,可以得到系统的单位脉冲响应曲线,如图3-15所示。在图3-15中,x轴和y轴都是自动地进行标注的。如果希望对x轴和y轴做不同的标注,则需要改变阶跃命令。例如,如果需要在x轴上标注"t Sec",在y轴上标注"Input and Output",则应利用带有左端变量的阶跃响应命令,其源程序如下:
MATLAB Program 3-3
num=[0 1 1];
den=[1 0.2 1];
impulse(num,den);
grid;
title('G(s)=s/(s^2+0.2s+1)的单位脉冲响应')
图3-15 用 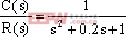 的单位阶跃响应求得的单位脉冲响应曲线 的单位阶跃响应求得的单位脉冲响应曲线 |
c=step(num,den,t)
或者
[y,x,t]=step(num,den,t)
参见MATLAB Program3-4。
3.7.6斜坡响应
在MATLAB中没有斜坡响应命令,因此,需要利用阶跃响应命令求斜坡响应。特别是当求传递函数系统G(s)的斜坡响应时,可以先用s除G(s),再利用阶跃响应命令。例如,考虑下列闭环系统:
对于单位斜坡输入量,R(s)=1/(s2),因此 为了得到系统的单位斜坡响应,往MATLAB程序中输入下列分子和分母:
num=[0 0 0 1];
den=[1 1 1 0];
并应用阶跃响应命令。参见MATLAB Program3-4,利用此程序获得的响应曲线如图3-16所示。其源程序如下: MATLAB Program 3-4
num=[0 0 0 1];
den=[1 1 1 0];
t=0:0.1:7;
c=step(num,den,t);
plot(t,c,'o',t,t,'-')
grid;
title('Unit-Ramp Response Curve for System G(s)=1/(s^2+s+1)')
xlabel('t Sec')
ylabel('Input and Output') |