滞后不确定系统的无辨识自适应智能控制方法
滞后不确定系统的无辨识自适应智能控制方法
针对带有大纯滞后、不确定性的工业过程,提出一种无需辨识的自适应智能控制方法。该方法不需要对过程建立数学模型,只要检测过程的实际输出和期望输出,通过模糊预测控制来修正单神经元自适应PSD控制律,即可以对滞后不确定、建模困难的工业过程实现自适应控制。仿真结果表明用该方法控制滞后不确定系统具有简单、实用、鲁棒性强的特点。
关键词:滞后不确定系统 单神经元 PSD控制 模糊预测控制
1 引言
含有纯滞后的不确定过程是石油、化工、冶金等工业生产中广泛存在的一类复杂过程。它的控制问题一直是困扰控制理论和控制工程实践的难题。目前对滞后不确定对象的控制主要采用自适应控制、鲁棒控制、预测控制等[1],然而这些方法都是建立在过程模型确定的基础上,不能对那些无法精确建模的复杂控制过程进行有效的控制。Marsik和Strejc[2]于1983年根据控制过程的几何特性建立性能指标,提出了无需辨识的自适应PSD(比例、求和、微分)控制算法,这种方法无需辨识对象的参数,只要检测过程实际输出及期望输出就可以形成闭环控制,可是该方法不能解决大纯滞后问题。以该算法调整神经元的增益形成的单神经元自适应PSD控制[3,4]比前者具有更强的适应性和鲁棒性,且算法简单,易于实时控制,在一定范围内对滞后不确定过程能实现较好的控制。但单神经元自适应PSD算法仍然是用过程当前和过去的信息来确定当前的控制动作,不能预测过程未来的输出及变化趋势,当滞后步数继续增大时,仅仅依靠增益和权值的自适应调整无法对大滞后不确定过程进行满意的控制。
针对以上问题,将模糊预测控制引入滞后不确定过程的控制中。利用模糊控制良好的动态特性和鲁棒性[5],以及其在处理具有不确定性控制问题上的独到优势,用模糊预测控制器预测过程未来的输出及变化趋势,并给出相应的预测控制量,以模糊预测来修正单神经元自适应PSD控制律构成无需辨识的自适应智能控制系统。仿真结果表明,该控制方法对滞后不确定系统具有良好的跟踪调节特性和较强的自适应能力。
2 无辨识自适应智能控制系统设计
用于控制滞后不确定过程的无辨识自适应智能控制系统结构图如图1所示。整个系统由两部分组成,单神经元自适应PSD控制(虚线框所示)和模糊预测控制(点划线框所示)。其中单神经元自适应PSD控制器是主控制器,神经元本身具有自适应、自学习的能力,采用Marsik和Strejc提出的无辨识自适应PSD算法对神经元的增益进行在线调整,增强了对滞后不确定过程的适应性和鲁棒性。模糊预测控制器的作用是在不增加对过程模型要求的基础上,根据过程的输入输出信息预测出控制量,来修正单神经元自适应PSD控制量,使调节器提前动作,从而使整个控制算法适用于大滞后不确定过程的控制。
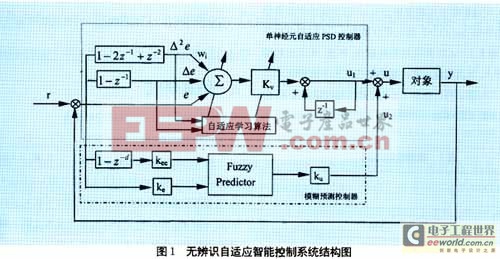
2.1 单神经元自适应PSD控制器
图1中神经元权值wi的学习采用有监督的Hebb学习规则,为保证算法的收敛性和鲁棒性,对学习算法进行规范化处理。引用自适应PSD控制算法对增益kv(t)进行自调整,构成具有自学习、自组织和强鲁棒性的新型单神经元自适应PSD控制算法。其控制算法归纳如下:
式中r(t)为给定信号,u(t)为控制器输出,y(t)为对象的实际输出,xi(t)(i=1,2,Λ,n)为神经元的输入状态,wi(t)为对应于xi(t)的加权系数,ηi为学习速度。根据PSD控制规律可以得到控制增益kv(t)的在线调整算式如下:
其中0.025≤c≤0.05,0.005≤L≤0.1
由于神经元自适应PSD控制算法中增益系数可在线调整,它的可调参数选择范围较大,提高了控制系统的鲁棒性和自适应能力。对滞后不确定系统的仿真实验表明,在滞后步数不太大时,通过调整kv(0)、Tv(0)的初值,在一定范围内可以改善系统的动态特性,取得较满意的控制效果。但若进一步增大滞后步数,依靠kv(t)、Tv(t)的自调整及权值的自学习也难以抑制系统过大的超调和振荡,甚至无法对滞后不确定系统进行控制。鉴于此引入模糊预测控制器,以模糊预测控制量来修正单神经元自适应PSD控制量,从而对大滞后不确定系统进行有效的控制。
2.2 模糊预测控制器
模糊预测控制器中模糊预测的功能是根据过程实际输出逼近期望输出来估计控制系统的性能并修正神经元自适应PSD控制律。具体设计如下:
(1)模糊化。模糊预测控制器的输入是过程实际输出与期望输出间的偏差e(t)及该偏差在t时刻和t-d时刻的变化Δe(t),输出是控制补偿量u2(t)。e(t)和Δe(t)描述为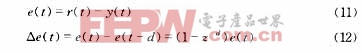
其中d为纯滞后时间。取ke、kec分别为e(t)和Δe(t)的量化因子,ku为预测输出的比例因子。E、EC和U2分别是e(t)、Δe(t)和u2(t)的语言变量。E、EC各取三个语言变量分别为N、S、P,U2取七个语言变量为NB、NM、NS、ZR、PS、PM、PB。输入E、EC和输出U2均采用三角形均匀分布的隶属函数。
(2)模糊控制规则。模糊预测控制的模糊规则为
if E(t) is A and EC(t) is B then U2(t) is C
其中A,B,C分别为e(t)、Δe(t)和u2(t)的模糊集。如果t时刻e(t)>0,即过程输出比期望输出小,且过程输出有比期望输出更小的趋势即Δe(t)>0,那么可以推断t-d时刻过程的输入太小,应增大t-d时刻控制器的输出;相反,如果过程输出比期望输出大,且过程输出有比期望输出更大的趋势即e(t)<0且Δe(t)<0,那么可以推断t-d时刻过程的输入太大,应减小t-d时刻控制器的输出。同理可以构造出模糊推理规则表如表1。
模拟电路 模拟芯片 德州仪器 放大器 ADI 模拟电子 相关文章:
- 12位串行A/D转换器MAX187的应用(10-06)
- AGC中频放大器设计(下)(10-07)
- 低功耗、3V工作电压、精度0.05% 的A/D变换器(10-09)
- PIC16C5X单片机睡眠状态的键唤醒方法(11-16)
- 用简化方法对高可用性系统中的电源进行数字化管理(10-02)
- 利用GM6801实现智能快速充电器设计(11-20)
