智能仪表非线性自动校正方法探讨

在称重仪表中，最小测量值x0=0kg，对应的零点值N0≠0，而且会随着环境温度的变化而变化，实际测量时，各校正点Xi对应的A/D转换值Ni(i=1,2,3,…)也会因零点的变化而相应发生变化。也就是说，环境温度变化后，实际测量时，当被测量为 Xi时，仪表内部获取的A/D转换值不再是校正时的Ni，从而使得按上述校正方程式(2)或式(3)求取的测量校正值是错误的或不准确的。

　　实验证明，称重仪表的零点值N0受环境温度的影响较大，而其非线性特性曲线受环境温度的影响较小[7]。如图1中所示，N0发生变化后，可以近似认为非线性特性曲线OM只是适当左移或右移。也就是说，尽管N0是变化的，而Ni-N0(i=1,2,3，… )可以认为是不变的。

　　一般来说，每天的不同时刻都会存在一定的温差，但每天的温度变化都非常缓慢，称重仪表的零点在使用过程中的变化也非常缓慢。根据这个特点，我们完全可以用软件的方法实现零点跟踪，即在某个较短的时间段(如0.5s)内，若采样到的A/D值n与之前的零点N0之差的绝对值不超过某个较小的数值，则令N0=n。

　　鉴于仪表的零点值N0受环境温度的影响较大，非线性校正方程要作相应的修正：不管是校正时还是实际测量时，均把得到的A/D转换值减去零点值N0。此时，点斜式校正方程修正为：

2.2 校正方程参数的存储结构

　　对于点斜式校正方程式(4)而言，要存入仪表内存的校正方程参数为：Mi-1、Xi-1和ki(i=l,2,3，…m;M0=X0=0)，可用一个三维数组形式的表格存放。

　　对于两点式校正方程式(5)而言，要存入仪表内存的校正方程参数为：Mi、Xi(i=0,1,2,3，…，m;M0=x0=0)，可用一个二维数组形式的表格存放。

　　考虑到M0=x0=0，故M0和X0不必保存，但应在表首位置存储校正点数j。两个校正方程的校正参数在仪表内存中的存储结构分别如图2所示，其中Tab.l和Tab.2分别表示内存参数表首地址。

　　2.3 非线性自动校正

　　从两个校正方程可以看出，点斜式只要做一次乘法运算，而两点式要做一次乘法运算和一次除法运算。考虑到：计算斜率ki时，为了保证测量精度，小数点后需要保留足够的位数，视具体情况而定;而智能仪表中采用的微控制器通常不方便做小数乘法运算，而且位数越多、运算越耗时;另外，当分段数大于3时，点斜式比两点式所需内存空间要多。因此，对于在线实时校正的智能仪表来说，采用两点式校正方程往往更合适一些。这里选用式(5)作为校正方程。为了描述时区分校正方程中的变量和仪表内存中存储的校正参数，对校正方程做如下变量代换，令a=Xi-1，b=Xi，C=Mi-1,d=Mi，则校正方程式(5)变为：

　　称重计量时的非线性校正要解决以下三个问题。

　　①如何找出N位于哪一个直线段，考虑到校正点数不会太多，可采用简单的顺序查找法。

　　②在没有进行校正前，仪表如何显示实测重量。

　　按全量程线性处理，即把量程的最大值Xm作为唯一校正点，但校正点数j记为0，表示未进行过校正。因此，仪表内存参数表初始化时，j处保存0、M1处保存Nm-N0、X1处保存Xm和Xm是可以预知的，而N0也可以估算出来或通过实测获得。

　　③当实际称量物体的重量超过最大校准点重量时，仪表如何显示实测重量。

　　按最大校准点求得的校正参数进行校正。因此，称重仪表(电子衡器)称重计量和校准时的非线性自动校正程序流程分别如图3和图4所示。

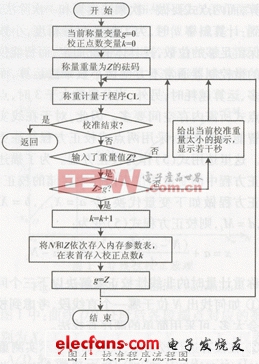
　　称重仪表(电子衡器)的校准过程如下：

　　①在称重仪表预热后，按校准>功能键(为安全起见，可要求输入一串验证码)，进入校准状态，此时仪表按原校准参数显示重量值;

　　②称量重。