智能仪表非线性自动校正方法探讨

　　智能仪表的模拟输入通道一般由传感器、前置放大电路、有源滤波器、采样保持电路(S/H)、A/D转换器和微机系统等电路组成[1]。由于电子元器件性能参数的离散性、稳定性和温度敏感性等问题，目前还得不到根本的解决。因此，从传感器到A/D 转换之间的任何一个环节都存在非线性的问题，使得A/D转换值n与被测量x不成线性关系，即n≠ax+b(a、b为常数)[2]。如果不解决这种非线性问题，将会严重影响智能仪表的测量精度。常用的非线性校正方法有校正函数法、查表法和模型校正法[s]。

　　① 校正函数法要求传感器的输入/输出特性能用数学解析式表示，且输入通道的其它环节可认为是线性的。事实上，很多传感器的输入/输出特性很难用解析式表示，并且如果解析式计算太复杂，还会严重影响测量速度。因此，校正函数法的应用受到较大的局限[4]。

　　② 查表法必须针对每一个传感器进行校正，而且需要把大量的校正数据制成表格存入仪表内存。而一般的智能仪表的内存非常有限;当因故更换传感器时，需要重新校正、修订内存中的表格数据，应用起来也非常不方便[5]。

　　③ 模型校正法的基本原理是设法找到一个近似函数g1(x)或多个分段近似函数g1(x)、g2(x)、g3(x)、g4(x)等来代替原函数f(x)。模型校正法的关键是如何求出既能满足精度要求，又能满足计算简单的校正模型。通常校正模型计算太复杂会影响测量速度，所以采用模型校正法进行非线性校正时，往往采用离线处理的方式[6]。

　　针对智能仪表不便于进行复杂计算、内存有限和实时性要求高等特点，在比较了几种常用的非线性校正方法的基础上，通过对智能仪表的非线性特性曲线的一般性分析，运用分段直线逼近曲线的方法，给出了一种通用的智能仪表非线性自动校正算法。

　　1 非线性自动校正算法

　　采用分段直线方程的非线性校正原理如图l所示。设仪表的被测量用X表示，仪表中对应的灯D转换值用N表示，则曲线OM表示仪表的非线性特性曲线。现将曲线分成若干段，如果分段点的位置和分段数选取合适，则每一段曲线可近似看成是一直线段。这样，曲线OM就可看成是由若干直线段组成。如图中虚线段AB、BC可分别近似表示曲线AB和曲线BC。

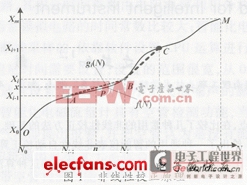
　　图1中：曲线OM分段后各段端点对应的被测信号分别为X0, X1,X2，…，Xi-1, Xi, Xi+1,…，Xm;仪表中对应的A/D转换值分别为N0, N1, N2，…，Ni, Ni+1, … ，Nm。其中，x0为被测量的最小值，Xm为被测量的最大值。显然线段AB的斜率为：

　　曲线段AB上的点(n,f(n))，可用直线段AB上的点P(n,x)近似表示，而点P满足：

　　式(2)、式(3)就是得到的分段直线校正方程。其中式(2)可称为点斜式校正方程，因为校正方程由线段上的端点(从Ni-1,Xi-1)和斜率ki决定;式(3)可称为两点式校正方程，因为校正方程由线段上的两端点(Ni-1, Xi-1)和(Ni,Xi)决定。

　　在校准时，若采用点斜式校正方程，则依次把校正方程参数(Ni-1,Xi-1)和ki(其中i=1,2,3，…，m)存入仪表的内存;若采用两点式校正方程，则依次把校正方程参数(Ni,Xi)(其中i=0,1,2,3，…，m)存入仪表的内存。在实际测量时只要先用程序判断仪表当前的A/D转换值N位于哪一个直线段，再从仪表内存中取出相应直线段的校正方程参数，则可由校正方程求出相应的测量值X。

　　从校正方程可以看出，测量值只与校正点的测量数据有关，而与包括传感器在内的模拟输入通道的各环节的非线性并无直接关系。因此，只要仪表的重复性或稳定性较好，即在不同时刻测量同一被测量X时，得到的A/D转换值N始终或基本保持不变，不论非线性是由于传感器还是因为模拟输入通道的其它环节引起的，都可以达到非线性校正的目的，从而保证仪表的测量精度。理论上讲，分的段数越多，仪表的测量精度就越高，但相应地，占用仪表的内存也越多，测量速度也会有少许影响，校准时也会稍微复杂。

　　需要指出的是，各种智能仪表存在较大的差异，实际应用中要视具体情况对非线性校正方程进行必要的修正。

　　2 在称重仪表中的应用

　　在电子衡器中，广泛采用的称重传感器是压力或拉力传感器。不论传感器的量程多大，其满度输出一般为2mV左右，因此，对于同一种类型(静态或动态)的电子衡器而言，往往可以采用通用的称重仪表。

　　电子衡器尤其是商用电子衡器，不仅对称重精度有很高的要求，而且对实时性也有较高的要求。因此，称重仪表的非线性校正必须采用在线方式。

　　2.1 非线性自动校正方程的修正

在称重仪表中，最小测量值x0=0kg，对应的零点值N0≠0，而且会随着环境温度的变化而变化，实际测量时，各校正点Xi对应的A/D转换值Ni(i=1,2,3,…)也会因零点的变化而相应发生变化。也