线性预测滤波器在抗多窄带干扰中的应用

摘要：在通信系统中，干扰抑制是一项基本的工作，对系统的稳定性起到重要的作用。详细讨论了关于线性预测技术在直扩系统中自适应抗窄带干扰的应用。理论仿真和实际验证结果表明，能够有效地抑制多个较强的窄带干扰，提高了系统的稳定性。此外，该算法资源消耗较少，工程实现容易，因此具有很强的实用性。
关键词：直扩；多窄带抗干扰；线性预测滤波器；FPGA

0 引言
直扩通信系统，由于其独特的抗干扰能力以及保密性能，在军事通信系统中备受青睐。但在今天频谱空间越来越拥挤，电磁环境越来越复杂的情况下，仅靠扩频增益已不足以对干扰进行抑制。特别在军事通信中还会受到敌方有意的窄带强干扰，这些人为干扰往往会超出导航接收机的抗干扰容限，系统将不能正常工作。因此，很有必要采用抗干扰技术对窄带干扰进行抑制，有效提高系统抗干扰性能。
目前针对窄带干扰的抑制技术主要可分为时域预测技术、变换域技术、码辅助技术。其中时域线性预测技术由于它能够抑制干扰较为彻底，滤波器具有线性相位，在工程中得到了更多的应用，然而由于线性预测的最佳抽头系数求解涉及到解维纳一霍夫方程，而高维的矩阵求逆对于工程实现来说是很难的，大量的论文研究给出了一些自适应算法，包括LMS，RLS等一些经典算法，但多数处于理论研究阶段，本文给出了基于FPGA的线性预测滤波器的简化实现技术，算法原理上采用基于LMS的递归求抽头系数，工程上采用符号LMS算法的实现方法，在实际扩频系统中，能够有效地自适应抑制窄带干扰，提高了系统的稳定性。

1 线性预测滤波器的基本原理
线性预测滤波器是自适应滤波器的一种，其基本思想是利用窄带信号和宽带信号在可预测性上的差距而达到干扰抑制的目的。因为窄带干扰时非高斯，样值间有很强的相关性，可以通过过去的样值来估计当前样值，而扩频信号频谱平坦，其样值间几乎不相关。当接收信号同时包含宽带有用信号和窄带十扰时，那么对接收信号进行预测，预测的值将主要是窄带信号的预测值，若从当前信号中减去预测值，将大大减小接收信号之中的窄带干扰，提高直扩系统的性能。
线性预测滤波器的两种基本结构是干扰基于状态空间的Kalman-Bucy预测器和抽头延迟线结构的有限脉冲响应的横向滤波器。在这里，主要讨论基于抽头延迟线的横向滤波器，它有两种结构，包括单边横向和双边横向，由于双边横向滤波器的改善性能更加优异，这里只给出双边横向的结构图，如图1所示。

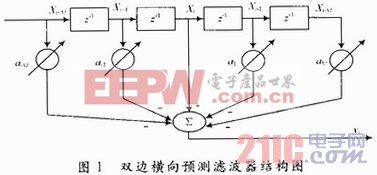
以图1中的双边横向滤波器来阐述线性预测滤波器的基本原理。在扩频系统中，现假设接收信号为：
x(t)=z(t)+j(t)+n(t) (1)
式中：z(t)=Ag(t)c(t)cos(ω0t)；j(t)=acos[(ω0+Ω)t+θ]；A，a为幅值；g(t)是信号码元，为Tg秒时间的二进制符号的随机序列；c(t)为扩频码序列，持续Tc秒，TcTg；ω0t为载波频率：Ω为频偏；θ为在[0，2π]上均匀分布的随机相位；n(t)为高斯噪声。
在iTc时刻，滤波器抽头取样值以及滤波器抽头系数如下：

式中W0是最佳抽头系数，式(5)即为熟知的维纳-霍夫等式。

2 线性预测滤波器在抗窄带干扰中的应用
2．1 线性预测滤波器的抗干扰特性研究
为了更好地阐述自适应线性预测滤波器的抗干扰特性。假设一带宽为20 MHz，信噪比为-32 dB的某扩频系统，信号带内出现了3个很强的点频干扰，每个干扰的干信比都在57 dB，采用16阶前后向的横向预测滤波器，抗干扰前后信号频谱如图2所示。

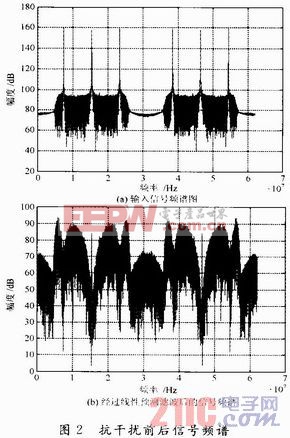
从滤波前后的频谱卜看，对于3个较强的点频干扰滤除较为彻底，在每个干扰位置处都产生了较深的陷波，较好地滤除了干扰，获得干扰抑制增益为60．23 dB，输出信噪比损失仅为1．9 dB，且当横向滤波器的阶数越高，预测的最佳抽头系数能够更加准确地重构出窄带干扰，获得的干扰抑制增益也就越高，当然付出的工程实现代价也随着增大。
2．2 符号LMS递归求解实现
从式(5)可以知道，求解维纳-霍夫方程的解涉及到矩阵求逆，而对于高达16阶的矩阵求逆，工程实现的难度可想而知，因此工程上大多采用LMS，RLS等自适应算法来递归求解，LMS算法由于其工程实现难度小，鲁棒性好的特点而得到广泛应用，在这里采用LMS算法。
LMS算法的统一形式如下：
w(n+1)=w(n)-μ(n)(n) (6)
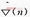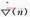式中：w(n+1)为第n+1次更新的滤波器系数；(n)为第n次迭代的梯度，通常用适当的估计值代替，若用=-2e(n)u(n)代替梯度的无记忆逼近，式中误差信号e(n)为期望输出d(n)与滤波器实际输出之间的误差，得到抽头系数的更新式子如式(7)所示：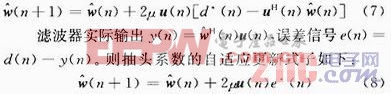

这里需要说明的是，在线性预测滤波器中，输出yi=xi-WTXi，d(n)为窄带干扰信号，扩频信号与噪声与d(n)相互独立，通过LMS重构的是接近于窄带干扰信号的d(n)，而不是能够重构出你想要的扩频信号，抗干扰完成是通过在实际系统中减去通过LMS迭代重构的窄带干扰信号而实现的。
工程实现中LMS的自适应滤波器算法复杂度比较高，一个M阶的滤波器在一个递归更新权值间隔内不仅要完成M次乘法滤波，还需要2M次乘法完成系数更新，这对于设计高阶自适应滤波器来说，对FPGA乘法器资源要求较高，因此采用符号LMS算法显得非常有必要。
符号LMS算法非常简单，也是利用随机梯度来达到最优解，但只给出其梯度迭代的方向，而并不给出具体的改变量，因此性能上不如常规LMS稳定，且误差可能较大。其迭代公式有两种，分别如下：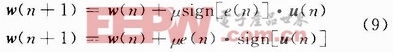

式(9)中，第一个公式是误差的符号LMS算法，第二个公式是信号的符号LMS算法，统称为符号LMS算法，两者的性能随机性很大，并不能说哪一种算法更好，在符号LMS算法中，由于步长因子的相乘也要乘法，只需要缩放即可，因此对于M阶自适应滤波器可节省系统M个乘法器，在实际系统中经常会采用符号LMS算法，在硬件资源受限时，往往能起到起死回生的作用，在这里具体工程实现中采用的是误差的符号LMS算法。

3 仿真与验证
某扩频系统，信号源强度为-127 dBm，系统带宽为20 MHz，加入带宽为2 MHz，中心频率为信号带内中心频率处的窄带干扰，强度为-70 dBm，即干信比为57 dB，信号经过下变频到中频信号，经过AD9248量化后，进入到在Xilinx XC4VLX160处理芯片设计的抗干扰系统内，利用Xilinx片上逻辑分析器ChipScopc对信号输入和输出采样，导入到Matlah中分析，图3为输入信号频谱和FPGA输出信号频谱图。