基于稀疏信号结构信息的压缩检测算法

引言

压缩感知(Compressive Sensing，CS)^[1-3]是一种新的信息获取理论。压缩感知理论建立在Candès，Romberg和Tao以及Donoho的工作上，他们提出并证明一个在某一种基下可以稀疏表示的信号可以通过一部分投影信息重构出来。与传统的奈奎斯特采样定理不同，该理论指出，只要信号是稀疏的或者在某个基下可压缩，就可以利用随机测量矩阵把高维空间上的信号稳定的嵌入到低维空间上。信号在低维空间上的投影包含了重构信号所需要的足够信息，可以用低维空间上的少量采样值精确重构出原始信号。

当前，对压缩感知理论的研究大多是以精确重构信号为目的。然而，在许多信号处理应用中，信号获取的最终目的并不是重构原始信号，而仅仅是完成一个检测决定^[4-9]，像在许多通信系统或者雷达系统中的信号检测任务^[10]。在许多情况下，由于压缩感知的采样值已经保持了原始信号的结构和相关信息，即使不精确重构信号也可以通过处理压缩感知的采样值完成信号的检测^[6,8]。

在基于压缩感知的稀疏信号检测具体算法方面，一种基于匹配追踪(Matching Pursuit，MP)的非相关检测和估计算法^[5]已经被提出。该算法通过比较利用部分重构算法得到的最大稀疏系数和利用蒙特卡洛模拟^[5]获得的最优门限之间的大小来完成检测任务。本文提出一种基于稀疏信号结构信息的检测方法，该方法可以分为两部分，包括一种基于压缩采样匹配追踪(Compressive Sampling Matching Pursuit，CoSaMP)^[11]的部分重构算法和一种新的检测判定方法。

本文内容安排如下。第二部分介绍压缩感知基础理论。第三部分我们提出并分析基于稀疏信号结构信息的压缩检测方法。第四部分我们通过仿真实验结果来验证提出方法的有效性。最后，第五部分总结工作并为以后的工作提出方向。

压缩感知理论

压缩感知理论主要包括信号的稀疏表示、编码测量和重构算法三个方

???????

基于稀疏信号结构信息的压缩检测算法

假设信号s是一个确定的已知的稀疏信号，我们考虑以下两种假设：

???????

本文中我们采用基于压缩采样匹配追

???????

???????

???????

对于目标信号s，对应稀疏系数值越大，其可重构出来的概率越大，反之，越小的稀疏系数越容易淹没于噪声中，从而无法重构出来。因此，我们引入可重构率的概念，具体定义如下式：

???????

表示位置相似度门限。若位置相似度大于所设门限，这时，需要通过幅值信息来判断目标信号的有无。文献^[4]通过比较部分重构算法所得的最大稀疏系数与所设门限的大小关系来判断目标信号的有无。在该算法中，门限是通过模特卡洛模拟的方法得到的，然而，实际中门限的设置比较困难，门限对噪声比较敏感，门限设置不恰当会严重影响检测性能。在本文中，我们提出一种新的方法来完成检测判决，该方法避免了门限的设置，同时仿真结果表明该方法具有很好的检测性能。具体方法如下：

???????

我们可以得到：

???????

仿真结果和分析

???????

首先我们验证本文提出的判决方法的有效性。我们对比不同信噪比下本文提出方法与文献^[4]采用的方法的检测成功率，这里部分重构算法我们分别采用文献^[4]提出的匹配追踪(MP)算法和改进的压缩采样匹配追踪(CoSaMP)算法，判决方法也分别采用文献^[4]的门限判决方法和本文提出的基于信号结构信息的判决方法。令采样点数M=80，信噪比SNR的变化范围为[-10,10]，步进为1。实验结果如图1所示。

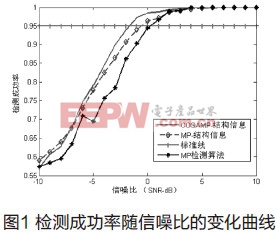
从图1可以看出，本文提出的基于结构信息的判决方法更具优势，同时，采用CoSaMP的部分重构算法比采用MP的部分重构算法获得的结构信息更可靠。下面我们研究测量点数对检测性能的影响。在仿真实验中，我们设迭代次数T=6，固定信噪比SNR=-2dB，图2为仿真实验结果。

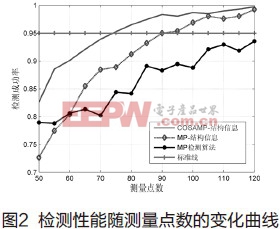
从图中可以看出，提出方法比原有方法更有优势，即使采用原有的部分重构算法，在判决部分采取本文提出方法，检测性能也有所提升。另外，从性能曲线的变化趋势，我们可以看出检测性能随测量点数的增加变得越来越好，这是由于测量点数增多，测量信号中包含的目标信号的结构信息越丰富，部分重构得到的估计信息更可靠。

然后，我们验证迭代次数对检测成功率及检测时间的影响。实验结果如图3和图4所示。

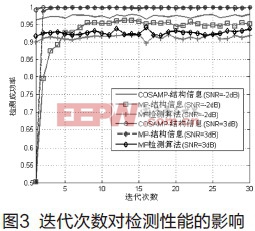
仿真实验中，对于图3所示的实验，我们考虑了SNR=-2dB和SNR=3dB的情况，测量点数为100;对于图4所示的实验，我们设置SNR=10dB，测量点数为100，检测时间定义为1000次检测所用的时间。从图3可以看出，本文提出方法检测性能很稳定，迭代次数对检测性能的影响很小，这是由于采用CoSaMP的部分重构算法在迭代次数很少的情况下就能获