利用信号调节器的抗混淆滤波器，实现混合信号、多模态传感器调节

号的白噪声带宽限制在5kHz。数字滤波器进一步将这种带宽降至2.5kHz，从而实现某个信白噪比。

由于图2所示两个模拟信号通路共用一个5kHz放大器，因此传感元件1的有效采样频率再一次为5kHz(假设对两个传感元件输出进行依次采样)。在这种情况下，2.5kHz到5kHz的所有模拟域噪声均进入0kHz到2.5kHz范围(有用频带)。但是，该频率范围内的均方根(RMS)噪声不受影响!换句话说，该电路的SNR与图1所示电路一样。

白噪声抗混淆滤波器：案例2

案例2中，我们假设有用信号带为1.25kHz，其为案例1的二分之一。也就是说，由于在1.25kHz以外没有我们想要的信号内容，并且噪声带宽限制改善了SNR，因此信号带得到了降低。假设5kHz放大器用于抗混淆，则我们会理所当然地得出结论：1.25kHz数字滤波器可降低带宽，并实现与图2所示电路一样的图1电路的SNR。但是，实际却并非如此。利用5kHz抗混淆滤波器，两种构架的采样域内RMS噪声相同，这的确没有错，但是它们的噪声密度却不同。使用独立信号通路时，采样信号的噪声密度为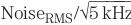，而公共信号通路的噪声密度为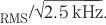。因此，在公共模拟信号通路中使用1.25kHz限带滤波器，会导致数字滤波器输出下的RMS噪声为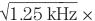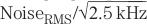。该噪声高于独立信号通路(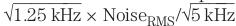)的RMS噪声。也就是说，公共信号通路的SNR比独立信号通路差。注意，这些RMS计算均假设使用理想的滤波器，也即0dB通带增益和无限抑止带衰减的滤波器。

仿真模型

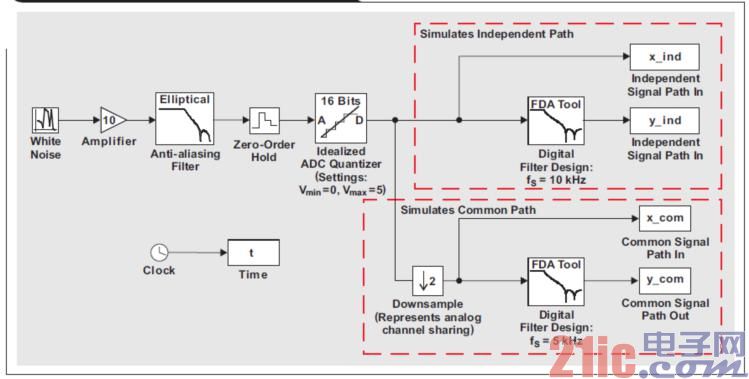
图3显示了一个MATLAB®/Simulink®模型，其用于分析信号通路构架对多余宽带白噪声的影响。该模型同时包括使用独立信号通路和公共信号通路的电路。注意，采样缩减2模块(downsample-by-2 block)用于表示公共信号通路依次采样的效果。假设模拟放大器增益为10，并且为是一个四阶椭圆低通滤波器。MATLAB/Simulink的FDA工具用于设计图3所示数字滤波器，其同样为四阶椭圆低通滤波器。1

表1总结了放大器带宽为5kHz到2.5kHz时1.25kHz数字滤波器的RMS噪声。MATLAB“std”函数用于计算RMS噪声。

表1 独立和公共信号通路的RMS噪声

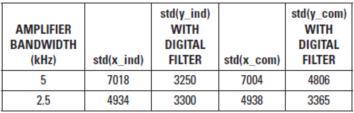
使用5kHz放大器带宽时，ADC输出RMS值及其采样缩减2值分别列举在“std(x_ind)”和“std(x_com)”两栏内，其大概相等。也就是说，采样缩减不影响RMS值。因此，如果采样缩减值在没有进一步数字滤波的情况下直接使用，公共信号通路的信白噪比与独立信号通路相同。

放大器带宽为2.5kHz时，数字滤波器输出的RMS值列举在“std(y_ind)”和“std(y_com)”栏内。由这些数据，我们可以清楚地知道，1.25kHz数字滤波器的效果取决于模拟抗混淆滤波器的频率。如果抗混淆滤波器的带宽为2.5kHz(相当于公共信号通路采样频率的一半)，则公共通路数字滤波器输出的噪声与独立信号通路中数字滤波器输出的噪声不相上下。但是，如果抗混淆滤波器的带宽为5kHz，则数字滤波器输出的RMS值非常不同，从而产生不同的信白噪比。

图3 MATLAB®/Simulink®仿真模型

结论

就多模态、混合信号传感器信号调节器而言，必须正确选择抗混淆滤波器的带宽，以消除多余信号和达到理想的SNR。如果使用∑-Δ调制器ADC，则必须丢弃那些在转换之后仍不稳定的ADC采样。这可以进一步降低有效采样率。

参考文献

1、《数字信号处理》，作者Alan V. Oppenheim和Ronald W. Schafer，Englewood Cliffs, NJ: Prentice-Hall，1975年。