改进的D-S理论在ETC系统中的应用研究
时间:08-21
来源:互联网
点击:
不停车收费系统即(NO STop ElectrONic Toll collection System,简称ETC)是智能交通系统(ITS)的重要内容,它的关键是利用车载智能识别卡与收费站车辆自动识别系统的无线电收发器之间,通过无线电波实现车辆自动识别和数据交换,获取通过车辆的类型和所属用户等相关数据,并由计算机系统控制指挥车辆通行,其过路过桥费通过计算机网络,从用户所在数据库中的专用账户或用户拥有的智能储值卡中自动交纳,从而实现不停车自动收费。整个系统运行的重要环节是正确提取通行车辆的车型和牌照数据,以及车载IC 卡中的信息,信息融合及判断的准确度决定了系统运行的可靠性。本文将给出改进的D-S 理论信息融合算法在ETC 系统中的应用研究。
1 D-S 证据理论概述及改进
Dempster-Shafer 证据理论(简称D-S 证据理论)源于20 世纪60 年代Dempster 在多值映射方面的工作,他将证据的信任函数与概率空间的概率的最大最小值相关联,构造了不确定推理模型的一般框架。此后Shafer 又在此基础上进行了扩展,形成了能够处理不确定、不精确、不完整信息的证据理论。它凭借其能够表示“不确定性”、“未知”等概念的优点,在数据融合中得到广泛重视。
1.1 D-S 证据理论概述
设有一个有限假设空间,Θ为空间中所有命题的穷举集合,D-S 理论用“识别框架(Frame. of Discernment)”描述构成整个假设空间的所有命题的集合Θ,识别框架中的各元素要求互相排斥,而集合中的命题称为识别框架的原命题。定义1 设Θ为给定识别框架,Ω=2Θ为Θ的幂集,则函数m:Ω→[0,1],在满足下列条件:
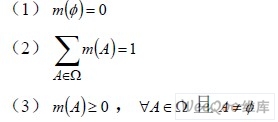
时,称m 为Ω 上的基本概率分配;?A∈Ω,m(A)称为基本概率分配函数(BPA),m(A)≥0的命题称为证据的焦元。
定义2 设Θ 为一识别框架,m(A)为Ω 上的基本概率分配函数,满足下列的函数称为信任函数:
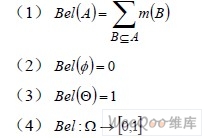
其中A 的信度函数为A 中每个子集的信度之和,Bel(A)表示对A 的总的信任程度,亦为可信度。
定义3 Bel 为给定信任函数,有一函数PL:
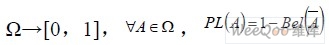
,则PL为A 的似然函数。即:
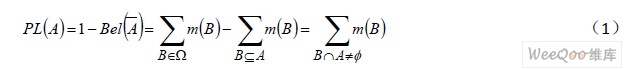
虽然D-S 证据理论在实际得到广泛的追捧,但在应用中人们发现其自身也存在一些不足和缺点,特别是在高冲突证据组合的时候会导致合成的结果违背直觉。前人如Zadeh 和Yager、Smets 他们也在这个问题上做了许多详细的研究,并提出了针对性的意见及妥善的改进方法。可惜随着科技的进步这一问题终究没有得到很好的解决。
1.2 D-S 证据理论的改进
D-S 的合成法则如下:
m1 与m2 是识别框架Θ 的两个独立证据,Ω 为Θ 的幂集,A、B 为幂集中的元素,则这两个证据组合后得到的组合证据为:

其中
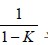
为归一化常数:
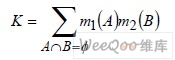
它的作用就是避免在合成时将非零的概率赋给空集Φ。
虽然D-S 理论有诸多优点,但在实际的应用中却不是令人满意,往往有时与直觉相违背,主要的原因是存在证据冲突,这是不可小觑的问题。所以做了如下的改进,取冲突权值为归一化常数的对数:

如果上述两个证据之间不存在冲突,则Cov(Bela,Belb)=∞;如果证据间完全冲突,则Cov(Bela,Belb)=0。在充分认识到证据间的冲突下,令σ=1-K 为冲突因子,当σ=0 时证据之间不存在任何冲突,当σ=1 时证据之间完全冲突,那么对D-S 的合成法则改进如下:
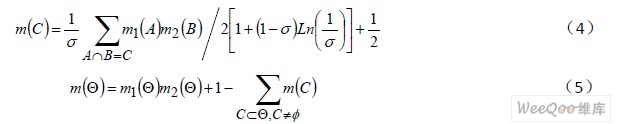
当融合的证据信息多于两个以上时,σ1,σ2,…,σn 为各个证据之间的冲突因子,则有:
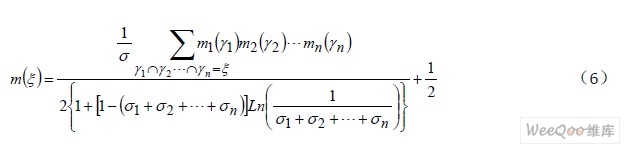
2 应用研究
在 ETC 系统中,合法车辆即为识别框架中唯一一个对象,届时,证据理论的基本问题就是从系统中的只读式非接触IC 卡、数码相机和车辆检测器等相关信息出发来进行信息融合,判明车辆的合法可能程度,并且这些相关信息均可作为的证据的载体。D-S 融合模型如图1 所示:
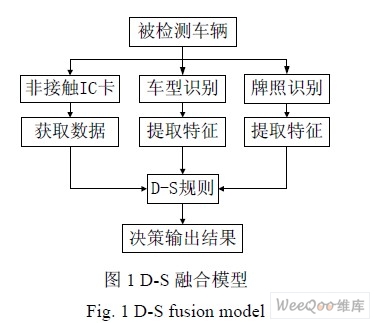
下面列举数据进行说明融合的过程:
假设识别框架U{车牌照X,车型Y,IC 卡数据Z},并提供两个证据m1 与m2(牌照加车型和卡号加车型)对命题的识别框架的支持度分别为:
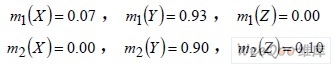
根据给出的数据,用早先的D-S 证据理论进行融合结果如下:
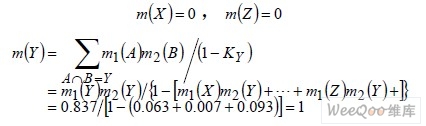
若用改进的D-S 的合成规则进行融合得出的结果又如下:
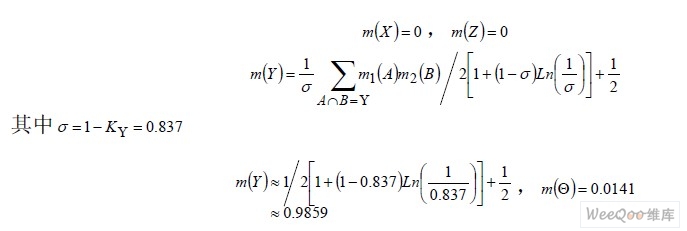
上述列举是在理想情况下得到的一组数据,在实际中数据的概率并非如此,现在对两种算法进行Matlab 仿真,取随机30 组数据,并进行计算。如表1、图2:

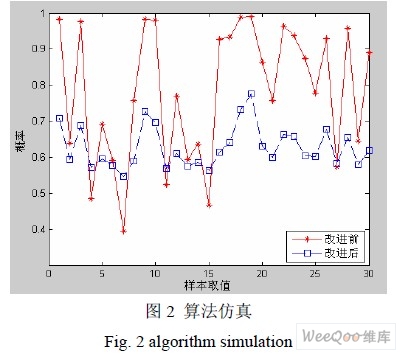
结果表明,通过改进的合成法则验证了预期要达到的结果,曲线的逼真度好于之前,使融合效果更为理想。
1 D-S 证据理论概述及改进
Dempster-Shafer 证据理论(简称D-S 证据理论)源于20 世纪60 年代Dempster 在多值映射方面的工作,他将证据的信任函数与概率空间的概率的最大最小值相关联,构造了不确定推理模型的一般框架。此后Shafer 又在此基础上进行了扩展,形成了能够处理不确定、不精确、不完整信息的证据理论。它凭借其能够表示“不确定性”、“未知”等概念的优点,在数据融合中得到广泛重视。
1.1 D-S 证据理论概述
设有一个有限假设空间,Θ为空间中所有命题的穷举集合,D-S 理论用“识别框架(Frame. of Discernment)”描述构成整个假设空间的所有命题的集合Θ,识别框架中的各元素要求互相排斥,而集合中的命题称为识别框架的原命题。定义1 设Θ为给定识别框架,Ω=2Θ为Θ的幂集,则函数m:Ω→[0,1],在满足下列条件:
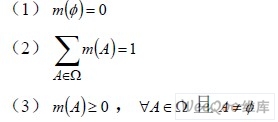
时,称m 为Ω 上的基本概率分配;?A∈Ω,m(A)称为基本概率分配函数(BPA),m(A)≥0的命题称为证据的焦元。
定义2 设Θ 为一识别框架,m(A)为Ω 上的基本概率分配函数,满足下列的函数称为信任函数:
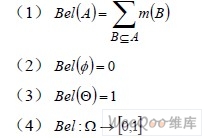
其中A 的信度函数为A 中每个子集的信度之和,Bel(A)表示对A 的总的信任程度,亦为可信度。
定义3 Bel 为给定信任函数,有一函数PL:
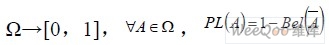
,则PL为A 的似然函数。即:
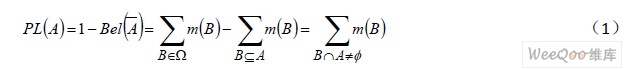
虽然D-S 证据理论在实际得到广泛的追捧,但在应用中人们发现其自身也存在一些不足和缺点,特别是在高冲突证据组合的时候会导致合成的结果违背直觉。前人如Zadeh 和Yager、Smets 他们也在这个问题上做了许多详细的研究,并提出了针对性的意见及妥善的改进方法。可惜随着科技的进步这一问题终究没有得到很好的解决。
1.2 D-S 证据理论的改进
D-S 的合成法则如下:
m1 与m2 是识别框架Θ 的两个独立证据,Ω 为Θ 的幂集,A、B 为幂集中的元素,则这两个证据组合后得到的组合证据为:

其中
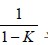
为归一化常数:
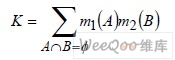
它的作用就是避免在合成时将非零的概率赋给空集Φ。
虽然D-S 理论有诸多优点,但在实际的应用中却不是令人满意,往往有时与直觉相违背,主要的原因是存在证据冲突,这是不可小觑的问题。所以做了如下的改进,取冲突权值为归一化常数的对数:

如果上述两个证据之间不存在冲突,则Cov(Bela,Belb)=∞;如果证据间完全冲突,则Cov(Bela,Belb)=0。在充分认识到证据间的冲突下,令σ=1-K 为冲突因子,当σ=0 时证据之间不存在任何冲突,当σ=1 时证据之间完全冲突,那么对D-S 的合成法则改进如下:
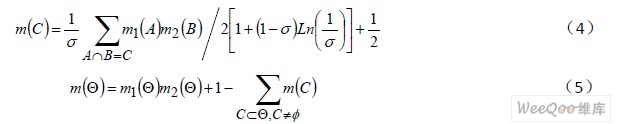
当融合的证据信息多于两个以上时,σ1,σ2,…,σn 为各个证据之间的冲突因子,则有:
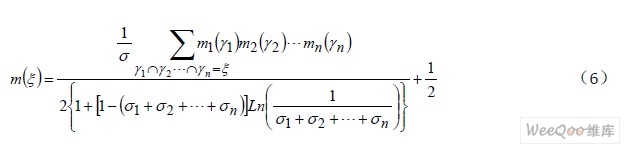
2 应用研究
在 ETC 系统中,合法车辆即为识别框架中唯一一个对象,届时,证据理论的基本问题就是从系统中的只读式非接触IC 卡、数码相机和车辆检测器等相关信息出发来进行信息融合,判明车辆的合法可能程度,并且这些相关信息均可作为的证据的载体。D-S 融合模型如图1 所示:

下面列举数据进行说明融合的过程:
假设识别框架U{车牌照X,车型Y,IC 卡数据Z},并提供两个证据m1 与m2(牌照加车型和卡号加车型)对命题的识别框架的支持度分别为:
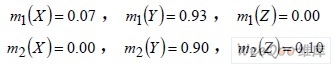
根据给出的数据,用早先的D-S 证据理论进行融合结果如下:
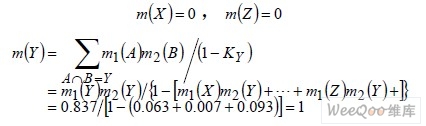
若用改进的D-S 的合成规则进行融合得出的结果又如下:
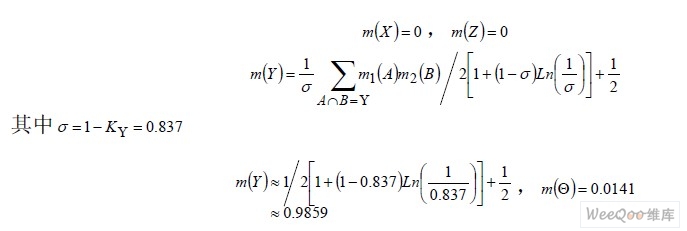
上述列举是在理想情况下得到的一组数据,在实际中数据的概率并非如此,现在对两种算法进行Matlab 仿真,取随机30 组数据,并进行计算。如表1、图2:


结果表明,通过改进的合成法则验证了预期要达到的结果,曲线的逼真度好于之前,使融合效果更为理想。
- 基于ARM的GSM远程监控系统(06-08)
- 基于ARM9-Linux平台的车载导航系统设计(04-07)
- 汽车仪表板照明需要具有丰富功能的开关稳压器(07-10)
- PolySwitch™ PPTC器件在汽车电子的应用方案(07-06)
- 平均电流模式DC/DC控制器在信息娱乐终端的应用(06-22)
- 低成本汽车导航系统的选择(07-07)
