基于GAL器件的步进电机控制器的研究与设计

步进电机广泛应用于对精度要求比较高的运动控制系统中，如机器人、打印机、软盘驱动器、绘图仪、机械阀门控制器等。目前，对步进电机的控制主要有由分散器件组成的环形脉冲分配器、软件环形脉冲分配器、专用集成芯片环形脉冲分配器等。分散器件组成的环形脉冲分配器体积比较大，同时由于分散器件的延时，其可靠性大大降低;软件环形分配器要占用主机的运行时间，降低了速度;专用集成芯片环形脉冲分配器集成度高、可靠性好，但其适应性受到限制，同时开发周期长、需求费用较高。通用阵列逻辑GAL(Generic Array Logic)是美国Lattice公司研制的一种电可擦除的可编程的新型PLD器件。近几年来，GAL以其高性能、高可靠性、可擦除及输出逻辑结构可组态等特性和100%的成品率，博得广大用户的信赖。它可以用来构成译码器、优先级编码器、多路开关、比较器、移位寄存器、计数器、总线仲裁器等。采用GAL器件对三相步进电机进行控制，不仅简化了系统的结构，降低了成本，而且编程灵活方便，提高了系统的可靠性，使系统具有更强的适应性。

1 三相六拍步进电机控制要求

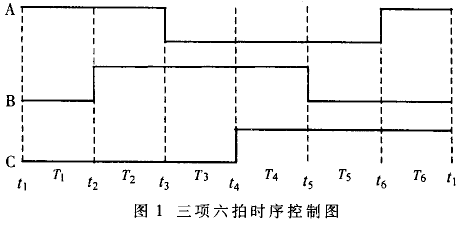
矩角特性是步进电机运行时一个很重要的参数，矩角特性好，步进电机启动转矩就大，运行不易失步。改善矩角特性一般通过增加步进电机的运行拍数来实现。三相六拍比三相二拍的矩角特性好一倍，因此在很多情况下，三相步进电机采用三相六拍运行方式。三相步进电机工作在三相六拍运行方式时，每个状态的变化使电机转动1/6齿距，三相激励规律为A-AB-B-BC-C-CA共六拍，对应时序如图1所示。A、B、C分别代表接到三相步进电机A相、B相、C相绕组的驱动脉冲。



通常，步进电机的脉冲控制是由逻辑电路实现的。在计算机控制的系统中，也可以通过编制程序，由扩展I/O口输出脉冲来决定电机的运行方式、方向及转速。这种方式电路简单、控制灵活，但占用CPU的时间过多，每次驱动电机时，PC机都得被占用。本文采用可编程逻辑器件(PLD)中的GALl6V8设计逻辑电路。在此，选三个控制信号：(1)启动控制信号S，当S=1时为停止，S=0为启动;(2)正反转控制信号D，当D=1时电机正转，D=0时电机反转;(3)转速切换信号R和C，当R=0、C=0时，频率为fck;R=1、C=1时，频率为fck/2。步进电机的转速通常都是通过改变时序脉冲的频率来控制的，所以这里用频率来表示转速的改变。由于GAL器件所有触发器的时钟是连在一起的，不能同时引入两种以上频率的时钟，因此从改造组合逻辑部分人手，达到对电动机转速的二分频控制。同理也可以实现四相八拍、五相十拍、六项十二拍的步进电机控制，这就比专用的集成电路功能更强。

2 采用GAL控制脉冲分配的逻辑设计

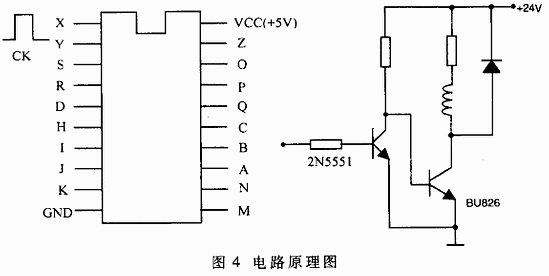
若采用集成电路芯片来实现三相六拍步进电机的控制，所用器件较多，电路一般比较复杂。为了满足电机转速的二分频，在同一时钟频率控制下，必须利用一个D型触发器，通过C参与组合逻辑来实现。其逻辑电路如图2所示。CK为控制信号，三个D型触发器的输出O、P、Q分别接步进电机的三项绕组。根据步进电机驱动相数及控制要求，必须有相应于相数的延迟触发器保持现态与次态间的转换过程。对此，可利用GAL中八个输出逻辑宏单元中的三个来完成，电机的工作状态(O、P、Q)中的现态与控制信号(S、R、D)可通过GAL的与、或阵列组合逻辑来完成。



2.1 逻辑控制状态表

按照电机的激励规律，在时序脉冲作用下，时序电路的状态将在六个状态中循环，驱动电机运转。这里用a、b、c、d、e、f分别表示其六个状态，即a=100、b=110、c=010、d=011、e=001、f=101。根据逻辑电路图可得其状态表，如表1所示。



2.2 状态真值表

由表1可得状态真值表，如表2所示。表中O、P、Q状态是在时钟脉冲控制下变化的，在控制变量的控制下，决定电机的启动、转向和转速大小。

2.3 卡诺图

在卡诺图中，输入变量分两排表示，变量的取值次序按照循环码排列。这种排列方法使得卡诺图中几何上相邻的两个小方块所代表的最小项只有一个变量不同这正是利用卡诺图化简逻辑函数的基础。



对于多变量输入，使用卡诺图时要注意以下几点：

(1)按照"最少、最大"的原则(即圈数最少，圈内的最小项个数尽可能多)圈起所有取值为1的相邻相。

(2)卡诺图中四个角与两对边的各项也是相邻的，卡诺图里上、下或左右部分中对称的项也是相邻的。

(3)每圈一个矩形圈时，必须至少包含一个在其它圈中未出现过的最小项，否则出现重复而得不到最简式。

(4)每一个取值为"1"的小方块都可以被圈多次，但不能遗漏，最小圈可以只包含一个小方块，即不能简化。

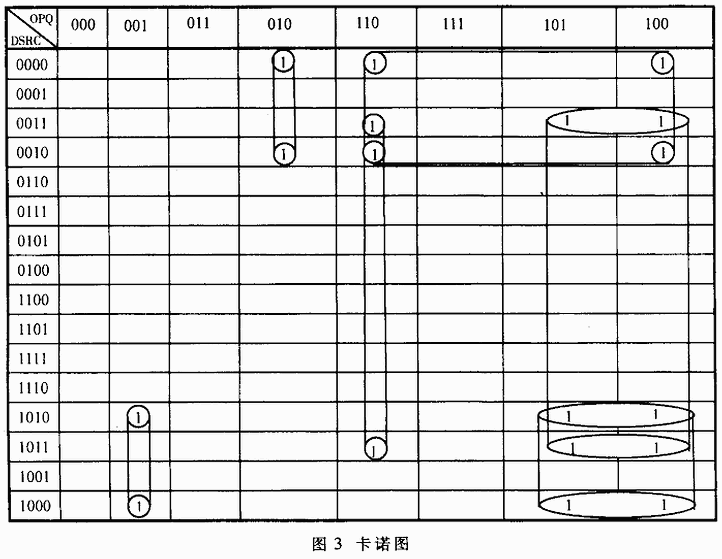
以O为例，由状态真值表可得其卡诺图，如图3所示。根据圈数和最小项可得其逻辑表达式为：

同样，也可以求得P、Q的逻辑表达式