基于最大峰度准则的非因果AR系统盲辨识
时间:11-24
来源:互联网
点击:
四、算法的收敛速度
下面考虑算法的收敛速度.不失一般性,假设平衡点为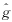 (i)=δ(τ),g(i)为偏离平衡点的一个迭代值.
(i)=δ(τ),g(i)为偏离平衡点的一个迭代值.
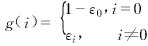 (18)
(18)
定义

则有,

≈(1-4ε0)/|1+ε-2ε0|2-1(推导中去掉了分子中ε,ε0所有的二次以上项)
≈(1-4ε0)|1-ε+2ε0|2-1
≈-2ε(推导中去掉了ε,ε0所有的二次以上项) (19)
由式(18)和(19),得到
J(g)-J(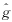 )∝‖g-
)∝‖g-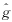 ‖2 (20)
‖2 (20)
可见在全局极值点附近,准则函数是以平方速度变化的.因此本文提出的基于梯度法寻优的学习算法在平衡点附近将线性收敛.从下节例1的图1和图2中可以看到在接近收敛点附近,辨识的各个参数都以几乎相同的斜率收敛到终值.

图1 反因果部分辨识过程

图2 因果部分辨识过程
五、仿真结果
此处给出两种典型情况的仿真结果,在所有仿真中加性观测噪声为高斯白噪声,输入信号是指数分布的随机过程(均值为零,λ=1),数据长度为3000.学习常数开始时为0.5,在学习过程中逐渐减小为0.1.对每个例子均为30次Monte Carlo实验.
例1.(非因果系统的辨识)真实AR模型为

它的极点位于-0.0506±j0.6532,-0.6988,和-1.7500±h1.3919,信噪比SNR=10dB辨识时取m=5和n=5,即因果MA部分和反因果MA部分分别比实际模型高两阶和三阶.辨识结果见表1和表2.
表1 非因果AR系统的因果部分辨识结果
表2 非因果AR系统的反因果部分辨识结果
图2和图3为最后一次Monte Carlo实验中b(i)和a(i)估计值的变化过程.由图中可以看到,在经过大约18次学习后,AR参数的估计值就收敛到真实值.

图3 g(i)的变化过程
例2 (反卷积:回响消除)假设房间的回响效果可以用以下的3阶MA模型表示,它的参数为h(0)=l,h(l)=0.5,h(2)=0.2,h(3)=0.1.为了减小截断效应,仿真时取反卷积滤波器的阶数为m=10.设g(i)=h(i)*a(i).
取反卷积滤波器的初始值为a(1)=1,a(2)=…=a(10)=0,迭代计算g(i)的结果如图3所示.由图可见,经过8次迭代,g(i)就趋近于一个δ函数,表示回响得到了很好的消除.其中g(i)的终值见表3第一行.它近似为δ(t).当初始值为a(1)=…=a(10)=0.1时g(i)的终值见表3第二行.它近似为δ(t-4).两个结果都是全局极值点.这个结果说明了算法是全局收敛的.
表3 g(i)的终值
六、结论
在文献的基础上,本文提出了基于二阶和四阶统计量的最大(规范化)峰度准则,并设计了基于这种准则的非因果AR系统辩识算法,这个算法同时也可以用于盲反卷积或盲均衡中.与文献未对算法作性能分析不同,本文证明了算法不但是全局收敛的,而且在平衡点附近将以线性速度进行收敛.仿真的结果验证了我们的结论.
下面考虑算法的收敛速度.不失一般性,假设平衡点为
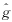 (i)=δ(τ),g(i)为偏离平衡点的一个迭代值.
(i)=δ(τ),g(i)为偏离平衡点的一个迭代值.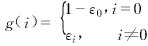 (18)
(18)定义

则有,

≈(1-4ε0)/|1+ε-2ε0|2-1(推导中去掉了分子中ε,ε0所有的二次以上项)
≈(1-4ε0)|1-ε+2ε0|2-1
≈-2ε(推导中去掉了ε,ε0所有的二次以上项) (19)
由式(18)和(19),得到
J(g)-J(
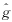 )∝‖g-
)∝‖g-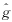 ‖2 (20)
‖2 (20)可见在全局极值点附近,准则函数是以平方速度变化的.因此本文提出的基于梯度法寻优的学习算法在平衡点附近将线性收敛.从下节例1的图1和图2中可以看到在接近收敛点附近,辨识的各个参数都以几乎相同的斜率收敛到终值.

图1 反因果部分辨识过程

图2 因果部分辨识过程
五、仿真结果
此处给出两种典型情况的仿真结果,在所有仿真中加性观测噪声为高斯白噪声,输入信号是指数分布的随机过程(均值为零,λ=1),数据长度为3000.学习常数开始时为0.5,在学习过程中逐渐减小为0.1.对每个例子均为30次Monte Carlo实验.
例1.(非因果系统的辨识)真实AR模型为

它的极点位于-0.0506±j0.6532,-0.6988,和-1.7500±h1.3919,信噪比SNR=10dB辨识时取m=5和n=5,即因果MA部分和反因果MA部分分别比实际模型高两阶和三阶.辨识结果见表1和表2.
表1 非因果AR系统的因果部分辨识结果
| a(1) | a(2) | a(3) | a(4) | a(5) | |
| 真实值 | 0.8 | 0.5 | 0.2 | 0 | 0 |
| 均值 | 0.7700 | 0.4524 | 0.2375 | -0.0296 | -0.0041 |
| 标准差 | 0.0654 | 0.0759 | 0.0741 | 0.0492 | 0.0322 |
表2 非因果AR系统的反因果部分辨识结果
| b(1) | b(2) | b(3) | b(4) | b(5) | |
| 真实值 | 0.7 | 0.2 | 0 | 0 | 0 |
| 均值 | 0.6738 | 0.2015 | 0.0261 | 0.0215 | 0.0019 |
| 标准差 | 0.0812 | 0.0677 | 0.0485 | 0.0419 | 0.0337 |
图2和图3为最后一次Monte Carlo实验中b(i)和a(i)估计值的变化过程.由图中可以看到,在经过大约18次学习后,AR参数的估计值就收敛到真实值.

图3 g(i)的变化过程
例2 (反卷积:回响消除)假设房间的回响效果可以用以下的3阶MA模型表示,它的参数为h(0)=l,h(l)=0.5,h(2)=0.2,h(3)=0.1.为了减小截断效应,仿真时取反卷积滤波器的阶数为m=10.设g(i)=h(i)*a(i).
取反卷积滤波器的初始值为a(1)=1,a(2)=…=a(10)=0,迭代计算g(i)的结果如图3所示.由图可见,经过8次迭代,g(i)就趋近于一个δ函数,表示回响得到了很好的消除.其中g(i)的终值见表3第一行.它近似为δ(t).当初始值为a(1)=…=a(10)=0.1时g(i)的终值见表3第二行.它近似为δ(t-4).两个结果都是全局极值点.这个结果说明了算法是全局收敛的.
表3 g(i)的终值
| g(1) | g(2) | g(3) | g(4) | g(5) | g(6) | g(7) | g(8) | g(9) | g(10) | |
| 终值 | 1.196 | 0.023 | 0.027 | 0.016 | 0.137 | -0.01 | -0.04 | -0.03 | -0.04 | -0.05 |
| 终值 | -0.01 | -0.02 | 0.001 | 0.057 | 1.296 | 0.023 | 0.025 | 0.023 | 0.151 | -0.02 |
六、结论
在文献的基础上,本文提出了基于二阶和四阶统计量的最大(规范化)峰度准则,并设计了基于这种准则的非因果AR系统辩识算法,这个算法同时也可以用于盲反卷积或盲均衡中.与文献未对算法作性能分析不同,本文证明了算法不但是全局收敛的,而且在平衡点附近将以线性速度进行收敛.仿真的结果验证了我们的结论.
- 基于nRF2401智能小区无线抄表系统集中器设计(04-30)
- 卫星电源分系统可靠性设计与研究(02-12)
- 新型锁相环芯片全面提升红外无线麦克风产品性能(05-04)
- 基于音频信号的轴承故障诊断方法(03-17)
- 基于nRF2401智能无线火灾监控系统设计(04-01)
- 提高实时系统数据采集质量的研究(04-09)
