基于音频信号的轴承故障诊断方法
时间:03-17
来源:互联网
点击:
轴承是机械设备中应用最为广泛的一种通用部件,也是最容易损坏的零件之一,它工作正常与否直接影响整台机器的性能,因而轴承故障诊断成为重要的研究课题和目前的研究热点[1-4]。在轴承故障诊断研究中,通常是对其工作时产生的振动信号[1]或音频信号[2-4]进行分析,以判断轴承运行状态。振动信号法通过安装在轴承座或箱体适当地方的加速度传感器获取轴承振动信号,并对其信号进行分析与处理,进而判断轴承是否运行正常。此方法的不足在于需要将加速度传感器固定在待检测的设备上,增加了成本,使用也不方便。音频信号的采集属于非接触式,只需要利用麦克风作为声音传感器,不但使用方便而且成本低廉,具有振动信号不可代替的优势。参考文献[2-4]研究表明,当轴承运行状态发生变化,音频信号特性也会随之变化时,因而对音频信号分析是一种有效、可行的轴承故障诊断方法。目前,基于音频信号的轴承故障诊断方法主要有:小波分析[2]、神经网络[3]和盲源分离方法[4]等。 隐马尔可夫模型HMM(Hidden Markov Model)是一种描述随机过程统计特性的概率模型,能够对多个观察样本进行有效融合而构成一个模型,具有较好的抗噪能力,在交通监测[5]、图像识别[6]、语音识别[7-8]以及基于振动信号的故障诊断[1]等领域中都得到了较好的应用,也是目前为止最有效的语音识别方法。而Mel频率倒谱系数MFCC(Mel Frequency CepstrumCoefficients)考虑了人耳听觉特性,能很好地反映音频信号特征,在语音识别、音频分类和检索研究领域应用十分广泛[8]。本文通过对音频信号的MFCC特征提取,分别采用DHMM(Discrete HMM)和CGHMM(Continuous Gaussian MixtureHMM)两种方法进行建模与诊断研究。DHMM方法对观测序列进行了量化处理,运算速度快,却降低了诊断精度。而CGHMM方法不需要量化,避免了量化带来的数据处理误差,提高了诊断精度,但减慢了运算速度。从总体上来看,两种方法都具有运算速度快、诊断精度高的优点,具有很好的应用前景。
1 理论基础
1.1 MFCC
Mel频率倒谱系数MFCC用于信号特征提取,其计算过程如下[8-9]:
(1) 确定每一帧信号的长度N及帧移,并对每一帧信号序列进行预处理(加窗、预加重等)。本文采用应用较广的汉明窗:
ω(n)=(1-α)-αcos(2πn/N) (1)
式中,0<α<1,通常取值为0.46。
(2) 将预处理后的信号进行快速傅立叶变换(FFT),将时域信号转换为频域信号,再计算其模的平方得到能量谱P[k],0≤k≤N-1。
(3) 选取滤波器个数为M,并定义最低频率接近零,最高频率为输入音频信号频率的一半,再根据mel(f)频率与实际线性频率f的关系mel( f )=2 595lg(1+f/700)计算出三角带通滤波器组Hm[k],则能量谱P[k]通过三角带通滤波器组Hm(k)后的输出为:
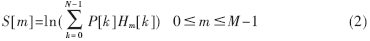
(4) 对S[m]进行离散余弦变换(DCT)即得到MFCC系数:
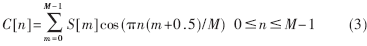
(5) 取C[1],C[2],…,C[V]作为MFCC参数,此处V是MFCC参数的维数,通常为12~16。
1.2 HMM
隐马尔可夫模型HMM是在Markov链的基础上发展起来的一种概率模型,由三个基本参数来描述。第一个参数为状态转移概率A={aij|1≤i,j≤N},aij=P(qt+1=Sj/qt=Si)表示从状态Si变化到状态Sj的转移概率,显然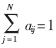 且aij≥0,其中,qt表示Markov链t时刻所处的状态,N为HMM状态数。第二个参数为观察值概率分布B={bj(k)|1≤j≤N, 1≤k≤M},bj(k)=P(Ok/qt=Sj)表示进入状态Sj时输出为Ok的概率,Ok表示观察值,M为可能的观察值数目。根据观察值序列的分布特点,HMM模型可分为离散DHMM和连续DHMM两大类。同时,如果观察值序列服从连续高斯混合密度函数分布,则为连续高斯混合密度CGHMM。最后一个参数是初始概率分布π={πi|1≤i≤N},πi=P(q1=si)表示Markov链从状态Si开始的概率,显然
且aij≥0,其中,qt表示Markov链t时刻所处的状态,N为HMM状态数。第二个参数为观察值概率分布B={bj(k)|1≤j≤N, 1≤k≤M},bj(k)=P(Ok/qt=Sj)表示进入状态Sj时输出为Ok的概率,Ok表示观察值,M为可能的观察值数目。根据观察值序列的分布特点,HMM模型可分为离散DHMM和连续DHMM两大类。同时,如果观察值序列服从连续高斯混合密度函数分布,则为连续高斯混合密度CGHMM。最后一个参数是初始概率分布π={πi|1≤i≤N},πi=P(q1=si)表示Markov链从状态Si开始的概率,显然
有了如上定义,HMM可描述为:
λ=(π,A,B) (4)
2 基于HMM的故障诊断
基于HMM的轴承故障音频信号诊断系统框图如图1所示,主要包括数据采集、特征提取、HMM训练和HMM诊断等部分。
1 理论基础
1.1 MFCC
Mel频率倒谱系数MFCC用于信号特征提取,其计算过程如下[8-9]:
(1) 确定每一帧信号的长度N及帧移,并对每一帧信号序列进行预处理(加窗、预加重等)。本文采用应用较广的汉明窗:
ω(n)=(1-α)-αcos(2πn/N) (1)
式中,0<α<1,通常取值为0.46。
(2) 将预处理后的信号进行快速傅立叶变换(FFT),将时域信号转换为频域信号,再计算其模的平方得到能量谱P[k],0≤k≤N-1。
(3) 选取滤波器个数为M,并定义最低频率接近零,最高频率为输入音频信号频率的一半,再根据mel(f)频率与实际线性频率f的关系mel( f )=2 595lg(1+f/700)计算出三角带通滤波器组Hm[k],则能量谱P[k]通过三角带通滤波器组Hm(k)后的输出为:
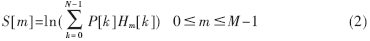
(4) 对S[m]进行离散余弦变换(DCT)即得到MFCC系数:
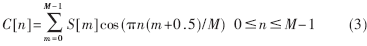
(5) 取C[1],C[2],…,C[V]作为MFCC参数,此处V是MFCC参数的维数,通常为12~16。
1.2 HMM
隐马尔可夫模型HMM是在Markov链的基础上发展起来的一种概率模型,由三个基本参数来描述。第一个参数为状态转移概率A={aij|1≤i,j≤N},aij=P(qt+1=Sj/qt=Si)表示从状态Si变化到状态Sj的转移概率,显然
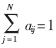 且aij≥0,其中,qt表示Markov链t时刻所处的状态,N为HMM状态数。第二个参数为观察值概率分布B={bj(k)|1≤j≤N, 1≤k≤M},bj(k)=P(Ok/qt=Sj)表示进入状态Sj时输出为Ok的概率,Ok表示观察值,M为可能的观察值数目。根据观察值序列的分布特点,HMM模型可分为离散DHMM和连续DHMM两大类。同时,如果观察值序列服从连续高斯混合密度函数分布,则为连续高斯混合密度CGHMM。最后一个参数是初始概率分布π={πi|1≤i≤N},πi=P(q1=si)表示Markov链从状态Si开始的概率,显然
且aij≥0,其中,qt表示Markov链t时刻所处的状态,N为HMM状态数。第二个参数为观察值概率分布B={bj(k)|1≤j≤N, 1≤k≤M},bj(k)=P(Ok/qt=Sj)表示进入状态Sj时输出为Ok的概率,Ok表示观察值,M为可能的观察值数目。根据观察值序列的分布特点,HMM模型可分为离散DHMM和连续DHMM两大类。同时,如果观察值序列服从连续高斯混合密度函数分布,则为连续高斯混合密度CGHMM。最后一个参数是初始概率分布π={πi|1≤i≤N},πi=P(q1=si)表示Markov链从状态Si开始的概率,显然
有了如上定义,HMM可描述为:
λ=(π,A,B) (4)
2 基于HMM的故障诊断
基于HMM的轴承故障音频信号诊断系统框图如图1所示,主要包括数据采集、特征提取、HMM训练和HMM诊断等部分。
- 多核及虚拟化技术在工业和安全领域的应用(05-23)
- 基于ARM核的AT75C220及其在指纹识别系统中的应用(05-24)
- 采用信号调理IC驱动应变片电桥传感器(05-26)
- 基于nRF2401智能无线火灾监控系统设计(04-01)
- 家居安防无线监控报警系统(04-02)
- 高精度压力测控系统的试验研究(04-08)
